
 |
 ) is the twelfth of Saturn's known satellites:
) is the twelfth of Saturn's known satellites:
orbit: 377,400 km from Saturn
diameter: 1120 km
mass: 1.05e21 kg
In Greek mythology Dione was the mother of Aphrodite (Venus)
by Zeus (Jupiter).
Discovered by Cassini in 1684.
Dione is the densest of Saturn's moons (aside from Titan, whose density is increased by gravitational compression). It is composed primarily of water ice but must have a considerable fraction of denser material like silicate rock.
Though somewhat smaller, Dione is otherwise very similar to Rhea. They both have similar compositions, albedo features and varied terrain. Both rotate synchronously and have dissimilar leading and trailing hemispheres.
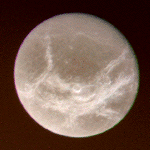
 On the trailing hemisphere there is a network
of bright streaks on a dark background and few visible craters
(left). The streaks
overlay the craters, indicating that they are newer.
On the trailing hemisphere there is a network
of bright streaks on a dark background and few visible craters
(left). The streaks
overlay the craters, indicating that they are newer.
The leading hemisphere is heavily cratered
and uniformly bright (right).
Like Callisto, the craters
lack the high relief features seen on the Moon and
Mercury.
This is interpreted as follows: shortly after its formation Dione was active. Some processes (ice volcanism?) resurfaced much of Dione leaving the the pattern of streaks, probably on the whole surface. Later, after the internal activity and resurfacing ceased, a much less intense series of impacts (which left craters too small to be seen in Voyager's images) occurred. This was concentrated on the leading hemisphere and wiped out the streak patterns but left them intact on the trailing hemisphere.
Helene orbits in Dione's leading Lagrange point.
 |
Helene is the thirteenth of Saturn's known satellites:
Discovered by Laques and Lecacheux in 1980 from ground-based observations.
Helene is in Dione's leading Lagrange point.