
 |
orbit: 9378 km from the center of Mars
diameter: 22.2 km (27 x 21.6 x 18.8)
mass: 1.08e16 kg
In Greek mythology, Phobos is one of the sons of Ares (Mars) and
Aphrodite (Venus).
"phobos" is Greek for "fear" (the root of "phobia").
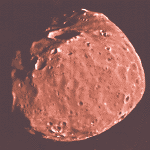
Discovered 1877 August 12 by Hall; photographed by Marriner 9 in 1971 and Viking 1 in 1977.
 Phobos orbits Mars below the
synchronous orbit radius. Thus it rises in the west,
moves very rapidly across the sky and sets in the east, usually twice a day.
It is so close to the surface that it cannot be seen above the horizon
from all points on the surface of Mars.
Phobos orbits Mars below the
synchronous orbit radius. Thus it rises in the west,
moves very rapidly across the sky and sets in the east, usually twice a day.
It is so close to the surface that it cannot be seen above the horizon
from all points on the surface of Mars.
And Phobos is doomed: because its orbit is below synchronous altitude tidal forces are lowering its orbit (current rate: about 1.8 meters per century). In about 40 million years it will either break up into a ring or crash onto the surface of Mars. (This is the opposite effect to that operating to raise the orbit of the Moon.)
Phobos and Deimos may be composed of carbon-rich rock like C-type asteroids. But their densities are so low that cannot be pure rock. They are more likely composed of a mixture of rock and ice. Both are heavily cratered.
The Soviet spacecraft Phobos 2 detected a faint but steady outgassing from Phobos. Unfortunately, Phobos 2 died before it could determine the nature of the material; water is the best bet.
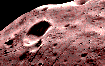
The most prominent feature on Phobos is the large crater named Stickney (the maiden name of Hall's wife). Like Mimas's crater Herschel (on a smaller scale) the impact that created Stickney must have almost shattered Phobos. The grooves and streaks on the surface were probably also caused by the Stickney impact.
 Phobos and Deimos are widely believed to be captured
asteroids. There is some speculation that
they originated in the outer solar system rather than in the main asteroid belt.
Phobos and Deimos are widely believed to be captured
asteroids. There is some speculation that
they originated in the outer solar system rather than in the main asteroid belt.
Phobos and Deimos may someday be useful as "space stations" from which to study Mars or as intermediate stops to and from the Martian surface; especially if the presence of ice is confirmed.