




Next: ΣΥΓΚΛΙΣΗ
Up: Η ΜΕΘΟΔΟΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Η μέθοδος της γραμμικής παρεμβολής :
- Συγκλίνει ταχύτερα από τη μέθοδο διχοτόμησης
- Δεν είναι υποχρεωτικό η ρίζα να εσωκλείεται μεταξύ των δύο αρχικών
τιμών.
Η διαδικασία εύρεσης της ρίζας με την μεθοδολογία που αναπτύξαμε
περιγράφεται από τον ακόλουθο αλγόριθμο:
Table:
Πρώτη παραλλαγή της μεθόδου γραμμικής παρεμβολής.
|
|
Στη διαδικασία που μόλις περιγράψαμε (Πίνακας
1.3) υπάρχει κάποιο αδύνατο σημείο, γιατί, όπως
γίνεται αντιληπτό, η τιμή 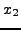 παραμένει σταθερή. Άρα πλησιάζουμε
τη ρίζα « μονόπλευρα » και αυτό έχει ως συνέπεια, μερικές φορές, η
σύγκλιση να είναι αρκετά αργή, βλ. Σχήμα 1.2
παραμένει σταθερή. Άρα πλησιάζουμε
τη ρίζα « μονόπλευρα » και αυτό έχει ως συνέπεια, μερικές φορές, η
σύγκλιση να είναι αρκετά αργή, βλ. Σχήμα 1.2
Υπάρχουν δυο εναλλακτικές διαδικασίες για τη διόρθωση της
μονόπλευρης σύγκλισης. Η πρώτη διαδικασία αλλάζει την επιλογή των
τιμών για το επόμενο βήμα, δηλαδή, αν από δυο τιμές 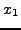 και
και 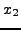 έχουμε υπολογίσει με τη χρήση της εξίσωσης (1.13) μια
τιμή
έχουμε υπολογίσει με τη χρήση της εξίσωσης (1.13) μια
τιμή 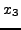 , χρησιμοποιούμε για το επόμενο βήμα την
, χρησιμοποιούμε για το επόμενο βήμα την 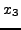 και
αυτήν από τις
και
αυτήν από τις 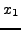 ,
, 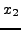 , για την οποία η
, για την οποία η
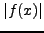 είναι μικρότερη. Επομένως, ο τροποποιημένος αλγόριθμος θα είναι:
είναι μικρότερη. Επομένως, ο τροποποιημένος αλγόριθμος θα είναι:
Table:
Δεύτερη παραλλαγή της μεθόδου γραμμικής παρεμβολής.
|
ΑΛΓΟΡΙΘΜΟΣ (ΙΙ) ΓΙΑ ΤΗΝ ΓΡΑΜΜΙΚΗ ΠΑΡΕΜΒΟΛΗ
H ρίζα δεν περικλείεται στο αρχικό διάστημα
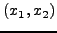
REPEAT
SET
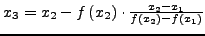
IF
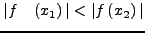
SET 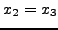
ELSE SET 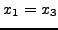
ENDIF
UNTIL

|
|
Η δεύτερη διαδικασία που βελτιώνει την ακρίβεια και την ταχύτητα
σύγκλισης είναι η αντικατάσταση της τιμής της 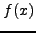 στο σταθερό
σημείο
στο σταθερό
σημείο 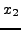 με την τιμή
με την τιμή 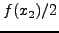 κοκ. Η διαδικασία αυτή
περιγράφεται στον παρακάτω τροποποιημένο αλγόριθμο:
κοκ. Η διαδικασία αυτή
περιγράφεται στον παρακάτω τροποποιημένο αλγόριθμο:
Table:
Εναλλακτικός αλγόριθμος για τη γραμμική παρεμβολή
|
ΑΛΓΟΡΙΘΜΟΣ (II) (τροποποιημενος )
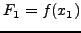
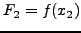
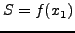
REPEAT
SET
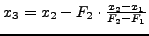
IF
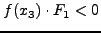
SET 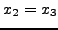
SET
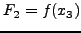
IF
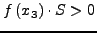
SET 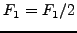
ENDIF
ELSE
SET 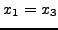
SET
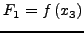
IF
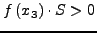
SET
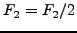
ENDIF
ENDIF
SET save = 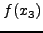
UNTIL
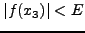
|
|





Next: ΣΥΓΚΛΙΣΗ
Up: Η ΜΕΘΟΔΟΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() και
και ![]() έχουμε υπολογίσει με τη χρήση της εξίσωσης (1.13) μια
τιμή
έχουμε υπολογίσει με τη χρήση της εξίσωσης (1.13) μια
τιμή ![]() , χρησιμοποιούμε για το επόμενο βήμα την
, χρησιμοποιούμε για το επόμενο βήμα την ![]() και
αυτήν από τις
και
αυτήν από τις ![]() ,
, ![]() , για την οποία η
, για την οποία η
![]() είναι μικρότερη. Επομένως, ο τροποποιημένος αλγόριθμος θα είναι:
είναι μικρότερη. Επομένως, ο τροποποιημένος αλγόριθμος θα είναι:
![]() στο σταθερό
σημείο
στο σταθερό
σημείο ![]() με την τιμή
με την τιμή ![]() κοκ. Η διαδικασία αυτή
περιγράφεται στον παρακάτω τροποποιημένο αλγόριθμο:
κοκ. Η διαδικασία αυτή
περιγράφεται στον παρακάτω τροποποιημένο αλγόριθμο: