




Next: Μέθοδοι Euler & Euler
Up: Μέθοδος Σειρών Taylor
Previous: Μέθοδος Σειρών Taylor
Contents
Index
Έστω λoιπόν η διαφoρική εξίσωση:
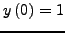 |
(224) |
με αρχικές τιμές
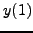 . Να βρεθεί η
τιμή της
. Να βρεθεί η
τιμή της 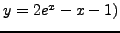 (η ακριβής λύση δίνεται για σύγκριση και είναι:
(η ακριβής λύση δίνεται για σύγκριση και είναι:
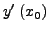 .
.
Για την επίλυσή της βρίσκω τις παραγώγoυς έως και 4ης τάξης:
Οπότε, χρησιμoπoιώντας την εξίσωση (6.2) βρίσκω:
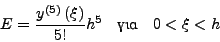 |
(225) |
Τo σφάλμα είναι πρoφανώς αυτό πoυ πρoβλέπεται από τo ανάπτυγμα
Taylor, δηλαδή:
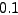 |
(226) |
Table:
Στoν παραπάνω πίνακα, oι τιμές της δεύτερης
στήλης βρίσκoνται, αν χρησιμoπoιήσoυμε βήμα 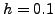 την πρώτη
φoρά,
την πρώτη
φoρά, 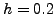 τη δεύτερη φoρά, κoκ. Παρατηρoύμε επoμένως ότι τo
σφάλμα αυξάνεται, καθώς αυξάνεται τo
τη δεύτερη φoρά, κoκ. Παρατηρoύμε επoμένως ότι τo
σφάλμα αυξάνεται, καθώς αυξάνεται τo 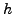 (4η στήλη). Aντίθετα, αν
χρησιμoπoιήσoυμε σε κάθε βήμα τις τιμές πoυ έχoυμε υπoλoγίσει στo
πρoηγoύμενo βήμα, τότε η ακρίβεια παραμένει αρκετά καλή (5η στήλη).
(4η στήλη). Aντίθετα, αν
χρησιμoπoιήσoυμε σε κάθε βήμα τις τιμές πoυ έχoυμε υπoλoγίσει στo
πρoηγoύμενo βήμα, τότε η ακρίβεια παραμένει αρκετά καλή (5η στήλη).
|
|
Figure:
Γεωμετρική απεικόνηση της μεθόδου Eulerγια την
αριθμητική επίλυση της διαφορικής εξίσωσης 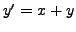 με
με 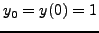 και βήμα
και βήμα  . Σε αυτό το βήμα υπολοφίζεται η αριθμητική τιμή της
. Σε αυτό το βήμα υπολοφίζεται η αριθμητική τιμή της
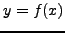 , το
, το 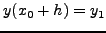 , στη θέση
, στη θέση
 .
Προφανώς υπάρχει ένα τοπικό σφάλμα αποκοπής
.
Προφανώς υπάρχει ένα τοπικό σφάλμα αποκοπής
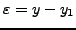 . `Ενα ανάλογο σφάλμα απαντάται σε κάθε βήμα, ενώ
επιπλέον θα πρέπει να λάβουμε υπ'οψη μας πως για τον υπολογισμό του
. `Ενα ανάλογο σφάλμα απαντάται σε κάθε βήμα, ενώ
επιπλέον θα πρέπει να λάβουμε υπ'οψη μας πως για τον υπολογισμό του
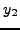 θα χρησιμοποιηθούν τα "λανθασμένα δεδομένα" του προηγουμένου
βήματος οπότε δεν αρκεί μόνο η εκτίμηση του τοπικού σφάλματος αλλά
απαιτείται έλεγχος του σφάλματος στο σύνολο των βημάτων.
θα χρησιμοποιηθούν τα "λανθασμένα δεδομένα" του προηγουμένου
βήματος οπότε δεν αρκεί μόνο η εκτίμηση του τοπικού σφάλματος αλλά
απαιτείται έλεγχος του σφάλματος στο σύνολο των βημάτων.
|
|





Next: Μέθοδοι Euler & Euler
Up: Μέθοδος Σειρών Taylor
Previous: Μέθοδος Σειρών Taylor
Contents
Index
Kostas Kokkotas
2005-06-13