




Next: ΠΡΟΒΛΗΜΑΤΑ
Up: Αριθμητική Επίλυση της Κυματικής
Previous: Δημιουργία των εξισώσεων διαφορών
Contents
Index
Οπως προαναφέραμε απαιτούνται οι αρχικές τιμές της 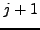 στις
γραμμές
στις
γραμμές 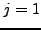 και
και 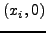 . Επειδή όμως η δεύτερη γραμμή δεν δίνεται
πάντα την υπολογίζουμε με βάση τις αρχικές συνθηκες. Αν
χρησιμοποιήσουμε πρώτης τάξης ανάπτυγμα Taylorτης
. Επειδή όμως η δεύτερη γραμμή δεν δίνεται
πάντα την υπολογίζουμε με βάση τις αρχικές συνθηκες. Αν
χρησιμοποιήσουμε πρώτης τάξης ανάπτυγμα Taylorτης 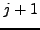 περι το σημείο
περι το σημείο 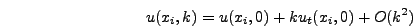 λαμβάνουμε
λαμβάνουμε
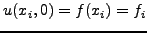 |
(368) |
Οπότε επειδή
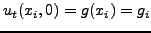 και
και
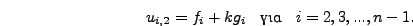 η
παραπάνω σχέση γράφεται
η
παραπάνω σχέση γράφεται
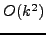 |
(369) |
Προφανώς η παραπάνω σχέση είναι προσεγγιστική και το αριθμητικό
σφάλμα που υπεισέρχεται μέσω της παραπάνω σχέσης είναι τάξης
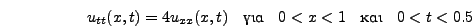 το οποίο διαδίδεται κατά την διάρκεια της αριθμητικής
εξέλιξης της εξίσωσης και γιαυτό είναι σημαντικό να θέτουμε απο την
αρχή αρκετά μικρή τιμή στο
το οποίο διαδίδεται κατά την διάρκεια της αριθμητικής
εξέλιξης της εξίσωσης και γιαυτό είναι σημαντικό να θέτουμε απο την
αρχή αρκετά μικρή τιμή στο 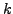 .
.
ΠΑΡΑΔΕΙΓΜΑ
Να λυθεί η κυματική εξίσωση της παλλόμενης χορδής
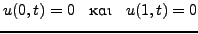 |
(370) |
με οριακές συνθήκες
ΛΥΣΗ
Για απλότητα θα χρησιμοποιήσουμε 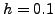 και
και 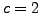 . Επειδή
. Επειδή 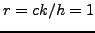 λαμβάνουμε
λαμβάνουμε 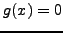 , επίσης επειδή
, επίσης επειδή 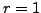 και
και  η σχέση
(8.28) γράφεται ως:
η σχέση
(8.28) γράφεται ως:
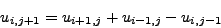 |
(372) |
Αντικαθιστώντας  στην εξίσωση (8.24) δημιουργούμε
την αρκετά απλή αναδρομική σχέση
στην εξίσωση (8.24) δημιουργούμε
την αρκετά απλή αναδρομική σχέση
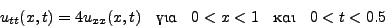 |
(373) |





Next: ΠΡΟΒΛΗΜΑΤΑ
Up: Αριθμητική Επίλυση της Κυματικής
Previous: Δημιουργία των εξισώσεων διαφορών
Contents
Index
Kostas Kokkotas
2005-06-13
![]() στις
γραμμές
στις
γραμμές ![]() και
και ![]() . Επειδή όμως η δεύτερη γραμμή δεν δίνεται
πάντα την υπολογίζουμε με βάση τις αρχικές συνθηκες. Αν
χρησιμοποιήσουμε πρώτης τάξης ανάπτυγμα Taylorτης
. Επειδή όμως η δεύτερη γραμμή δεν δίνεται
πάντα την υπολογίζουμε με βάση τις αρχικές συνθηκες. Αν
χρησιμοποιήσουμε πρώτης τάξης ανάπτυγμα Taylorτης ![]() περι το σημείο
περι το σημείο ![]() λαμβάνουμε
λαμβάνουμε
![]() και
και ![]() . Επειδή
. Επειδή ![]() λαμβάνουμε
λαμβάνουμε ![]() , επίσης επειδή
, επίσης επειδή ![]() και
και ![]() η σχέση
(8.28) γράφεται ως:
η σχέση
(8.28) γράφεται ως: