




Next: ΚΡΙΤΙΚΗ
Up: ΡΙΖΕΣ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
ΜΕΘΟΔΟΣ ΔΙΧΟΤΟΜΗΣΗΣ (BOLZANO)
Στο προηγούμενο παράδειγμα, ας προσπαθήσουμε να εφαρμόσουμε μια
απλοϊκή ίσως διαδικασία. Υποθέτουμε ότι το κεφάλαιο που κατατίθεται
κάθε μήνα είναι 1000 και το ποσό που έχουμε στόχο να
συλλέξουμε σε διάστημα 50 μηνών είναι 65000.
Αν δοκιμάσουμε λοιπόν για δυο τυχαίες (αλλά λογικές) τιμές του
επιτοκίου, έστω 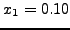 και
και 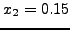 , θα βρούμε:
, θα βρούμε:
που σημαίνει ότι με επιτόκιο 0.10 (δηλαδή 10% ετησίως),
υπολειπόμεθα του στόχου μας κατά 3286.4, ενώ με επιτόκιο
0.15 τον ξεπερνούμε κατά 3881.8. Επομένως, η φυσική μας
επιλογή θα είναι να δοκιμάσουμε για επιτόκιο 0.125, δηλαδή μια τιμή
στο μέσο του διαστήματος 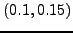 . Για επιτόκιο
. Για επιτόκιο 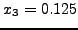 βρίσκουμε ότι:
βρίσκουμε ότι:
άρα απέχουμε από το στόχο μας μόνο κατά 174.5 ευρώ, ενώ
φαίνεται πλέον πως η σωστή τιμή του επιτοκίου βρίσκεται στο διάστημα
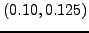 . Επομένως, επιλέγοντας μια τιμή στο μέσο του
διαστήματος, έστω
. Επομένως, επιλέγοντας μια τιμή στο μέσο του
διαστήματος, έστω
 , βρίσκουμε ότι
, βρίσκουμε ότι
Επομένως η σωστή τιμή βρίσκεται στο διάστημα
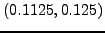 , άρα
μπορούμε να επιλέξουμε ένα νέο επιτόκιο, που θα είναι
, άρα
μπορούμε να επιλέξουμε ένα νέο επιτόκιο, που θα είναι
 , και να επαναλάβουμε την παραπάνω διαδικασία.
Μετά από μερικές ακόμη προσπάθειες, θα καταλήξουμε στην τιμή του
κεφαλαίου που επιθυμούμε να συγκεντρώσουμε μετά από καταθέσεις 50
μηνών.
, και να επαναλάβουμε την παραπάνω διαδικασία.
Μετά από μερικές ακόμη προσπάθειες, θα καταλήξουμε στην τιμή του
κεφαλαίου που επιθυμούμε να συγκεντρώσουμε μετά από καταθέσεις 50
μηνών.
Η `` απλοϊκή '' μέθοδος που χρησιμοποιήσαμε στο προηγούμενο
παράδειγμα αποτελεί μια από τις κλασικές μεθόδους εύρεσης ριζών
εξισώσεων και ονομάζεται μέθοδος διχοτόμησης ή
μέθοδος του Bolzano. Η παραπάνω διαδικασία μπορεί να
κωδικοποιηθεί ως ακολούθως :
`Εστω ότι μια ρίζα βρίσκεται στο διάστημα ![$[a_0,b_0]$](img58.png) , τότε
, τότε
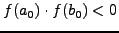 . Αν
. Αν
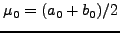 , τότε:
, τότε:
- (I) είτε
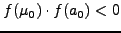
- (II) είτε
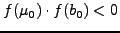
- (III) είτε
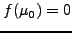 .
.
Αν ισχύει η (III), τότε έχει υπολογισθεί η ρίζα και σταματά η
διαδικασία, αλλιώς ορίζω νέο διάστημα
![\begin{displaymath}
\left[a_1,b_1 \right] = \left\{ {\begin{array}{l}
\left[\...
...0\right] \quad \mbox{αν} \quad (I) \\
\end{array}} \right.
\end{displaymath}](img64.png) |
(7) |
Figure:
Γραφική απεικόνιση της διαδικασίας που αναπτύχθηκε για τη
μέθοδο διχοτόμησης
|
|
Table:
Σχέδιο προγράμματος για τη εύρεση ρίζας μη-γραμμικής
εξίσωσης με τη μέθοδο της διχοτόμησης.
| REPEAT |
SET
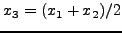 |
IF
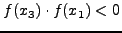 |
SET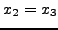 |
| ELSE |
SET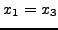 |
| ENDIF |
UNTIL
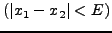 OR OR
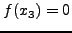 |
|
Subsections





Next: ΚΡΙΤΙΚΗ
Up: ΡΙΖΕΣ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() και
και ![]() , θα βρούμε:
, θα βρούμε:
![]() , τότε
, τότε
![]() . Αν
. Αν
![]() , τότε:
, τότε:
![\begin{displaymath}
\left[a_1,b_1 \right] = \left\{ {\begin{array}{l}
\left[\...
...0\right] \quad \mbox{αν} \quad (I) \\
\end{array}} \right.
\end{displaymath}](img64.png)