



Next: Temporal Behaviour of Turbulence
Up: In General About Seeing
Previous: In General About Seeing
Index
A description of the nature of the wavefront perturbations introduced by the atmosphere is provided by the Kolmogorov model based partly on the studies of turbulence by the Russian mathematician Andrei Kolmogorov. This model is supported by a variety of experimental measurements and is widely used in simulations of astronomical imaging. The model assumes that the wavefront perturbations are brought about by variations in the refractive index of the atmosphere. These refractive index variations lead directly to phase fluctuations described by
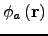 , but any amplitude fluctuations are only brought about as a second-order effect while the perturbed wavefronts propagate from the perturbing atmospheric layer to the telescope. For all reasonable models of the Earth's atmosphere at optical and infra-red wavelengths the instantaneous imaging performance is dominated by the phase fluctuations
, but any amplitude fluctuations are only brought about as a second-order effect while the perturbed wavefronts propagate from the perturbing atmospheric layer to the telescope. For all reasonable models of the Earth's atmosphere at optical and infra-red wavelengths the instantaneous imaging performance is dominated by the phase fluctuations
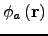 . The amplitude fluctuations described by
. The amplitude fluctuations described by
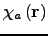 have negligible effect on the structure of the images seen in the focus of a large telescope.
have negligible effect on the structure of the images seen in the focus of a large telescope.
A turbulent field can be described statistically by a structure function:
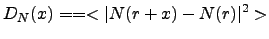 |
(2.1) |
where 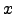 is separation of points,
is separation of points, 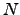 is any variable (e.g. tempereature, index of refraction, etc) and
is any variable (e.g. tempereature, index of refraction, etc) and 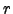 is position. Kolmogorov turbulence gives :
is position. Kolmogorov turbulence gives :
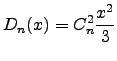 |
(2.2) |
where 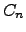 is the refractive index structure constant. From this, one can derive the phase structure function at the telescope aperture :
is the refractive index structure constant. From this, one can derive the phase structure function at the telescope aperture :
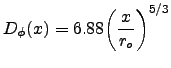 |
(2.3) |
where the coherence length 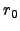 (also known as the Fried parameter) is :
(also known as the Fried parameter) is :
![$\displaystyle r_0 = 0.185 \lambda^{6/5} \cos^{3/5} z\bigg[ \int(C_n^2 dh) \bigg]^{-3/5}$](img70.png) |
(2.4) |
where 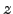 is zenith angle,
is zenith angle, 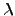 is wavelength. Using optics theory, one can convert
is wavelength. Using optics theory, one can convert 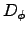 into an image shape. Physically,
into an image shape. Physically, 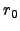 is inversely proportional to the image size from seeing :
is inversely proportional to the image size from seeing :
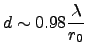 |
(2.5) |
as compared with the image size from diffraction-limited images :
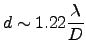 |
(2.6) |
Seeing dominates when 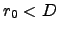 , a larger
, a larger 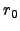 means better seeing. Seeing is more important than diffraction at shorter wavelengths (and for larger apertures), diffraction is more important at longer wavelengths (and for smaller apertures), the effects of diffraction and seeing cross over in the IR for most astronomical-sized telescopes (
means better seeing. Seeing is more important than diffraction at shorter wavelengths (and for larger apertures), diffraction is more important at longer wavelengths (and for smaller apertures), the effects of diffraction and seeing cross over in the IR for most astronomical-sized telescopes (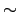 5 microns for 4m), the crossover falls at a shorter wavelength for smaller telescope or better seeing. The meaning of
5 microns for 4m), the crossover falls at a shorter wavelength for smaller telescope or better seeing. The meaning of 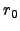 is in
is in
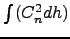 as you might expect, this varies from site to site and also in time. At most sites, there seems to be three regimes : "surface layer" (wind-surface interactions and manmade seeing), "planetary boundary layer" ( influenced by diurnal heating), and ``free atmosphere'' (high wind shears, 10 km is tropopause). A typical astronomical site has
as you might expect, this varies from site to site and also in time. At most sites, there seems to be three regimes : "surface layer" (wind-surface interactions and manmade seeing), "planetary boundary layer" ( influenced by diurnal heating), and ``free atmosphere'' (high wind shears, 10 km is tropopause). A typical astronomical site has
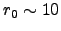 cm at 5000A. We also have to consider the coherence of the same turbulence pattern over the sky : coherence angle called the isoplanatic angle, and region over which the turbulence pattern is the same, is called the isoplanatic patch. So it is :
cm at 5000A. We also have to consider the coherence of the same turbulence pattern over the sky : coherence angle called the isoplanatic angle, and region over which the turbulence pattern is the same, is called the isoplanatic patch. So it is :
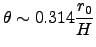 |
(2.7) |
where 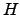 is the average distance of the seeing layer :
is the average distance of the seeing layer :
![$\displaystyle H = \sec z \bigg[ \frac{\int(C_n^2 h^{5/3} dh)}{\int (C_n^2 dh)}\bigg] ^{3/5}$](img79.png) |
(2.8) |
At a typical astronomical site where we have 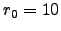 cm in the optical it will be
cm in the optical it will be
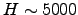 m and
m and
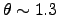 arcsec. In the infrared where it's
arcsec. In the infrared where it's
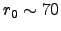 cm it will be
cm it will be
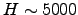 m and
m and
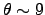 arcsec.
arcsec.
In reality, phase fluctuations in the atmosphere are only expected to follow the structure function shown in equation 2.3 over a finite range of length scales. The turbulent energy is injected at large scales by wind shear. The bulk of the wind shear is expected in discrete layers of the atmosphere, and the largest turbulent structures are expected to fit within one of these atmospheric layers. The length scale at which the structure function for Kolmogorov turbulence breaks down at large scales is called the outer scale of turbulence (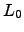 ). Several attempts have been made at measuring the size of this outer scale using a variety of different methods but there has been substantial variation in the measured values. The Von Karman model (Ishimaru, 1978) is expected to describe the form of the power spectrum for phase fluctuations on length scales larger than the outer scale. If the outer scale is larger than the telescope diameter, then most of the properties of short exposure astronomical images will not depend significantly on the precise size of the outer scale (although the amplitude of image motion is still weakly dependent on the outer scale size).
). Several attempts have been made at measuring the size of this outer scale using a variety of different methods but there has been substantial variation in the measured values. The Von Karman model (Ishimaru, 1978) is expected to describe the form of the power spectrum for phase fluctuations on length scales larger than the outer scale. If the outer scale is larger than the telescope diameter, then most of the properties of short exposure astronomical images will not depend significantly on the precise size of the outer scale (although the amplitude of image motion is still weakly dependent on the outer scale size).
At small scales (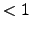
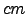 ) the turbulent energy in the atmosphere is dissipated through the viscosity of the air (Roddier, 1981). The length scale at which this becomes significant is called the inner scale of turbulence (
) the turbulent energy in the atmosphere is dissipated through the viscosity of the air (Roddier, 1981). The length scale at which this becomes significant is called the inner scale of turbulence (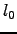 ). The steepness of the Kolmogorov turbulence spectrum means that any reduction in the power at such small length scales has relatively little effect on the imaging performance of optical and infra-red telescopes.
). The steepness of the Kolmogorov turbulence spectrum means that any reduction in the power at such small length scales has relatively little effect on the imaging performance of optical and infra-red telescopes.




Next: Temporal Behaviour of Turbulence
Up: In General About Seeing
Previous: In General About Seeing
Index
![]() ). Several attempts have been made at measuring the size of this outer scale using a variety of different methods but there has been substantial variation in the measured values. The Von Karman model (Ishimaru, 1978) is expected to describe the form of the power spectrum for phase fluctuations on length scales larger than the outer scale. If the outer scale is larger than the telescope diameter, then most of the properties of short exposure astronomical images will not depend significantly on the precise size of the outer scale (although the amplitude of image motion is still weakly dependent on the outer scale size).
). Several attempts have been made at measuring the size of this outer scale using a variety of different methods but there has been substantial variation in the measured values. The Von Karman model (Ishimaru, 1978) is expected to describe the form of the power spectrum for phase fluctuations on length scales larger than the outer scale. If the outer scale is larger than the telescope diameter, then most of the properties of short exposure astronomical images will not depend significantly on the precise size of the outer scale (although the amplitude of image motion is still weakly dependent on the outer scale size).
![]()
![]() ) the turbulent energy in the atmosphere is dissipated through the viscosity of the air (Roddier, 1981). The length scale at which this becomes significant is called the inner scale of turbulence (
) the turbulent energy in the atmosphere is dissipated through the viscosity of the air (Roddier, 1981). The length scale at which this becomes significant is called the inner scale of turbulence (![]() ). The steepness of the Kolmogorov turbulence spectrum means that any reduction in the power at such small length scales has relatively little effect on the imaging performance of optical and infra-red telescopes.
). The steepness of the Kolmogorov turbulence spectrum means that any reduction in the power at such small length scales has relatively little effect on the imaging performance of optical and infra-red telescopes.