Atmospheric refraction

The direction of light as it passes through the atmosphere is also changed because of refraction since the index of refraction changes through the atmosphere. The amount of change is characterized by Snell's law:

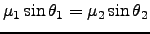$$\mu_1 \sin \theta_1 = \mu_2 \sin \theta_2$$ (1.8)

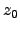Let $z_0$ be the true zenith distance, 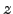$z$ be the observed zenith distance, 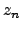$z_n$ be the observed zenith distance at layer 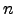$n$ in the atmosphere, 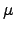$\mu$ be the index of refraction at the surface, and 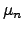$\mu_n$ be the index of refraction at layer 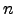$n$. At the top of the atmosphere it is :

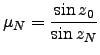$$\mu_{N}=\frac{\sin z_0}{\sin z_N}$$ (1.9)

At each infinitessimal layer we have :

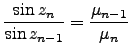$$\frac{\sin z_n}{\sin z_{n-1}} = \frac{\mu_{n-1}}{\mu_n}$$ (1.10)

as so on for each layer down to the lowest layer it will be :

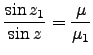$$\frac{\sin z_1}{\sin z} = \frac{\mu}{\mu_1}$$ (1.11)

By multipling equations 1.10 and 1.11 we get:

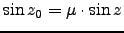$$\sin z_0 = \mu \cdot\sin z$$ (1.12)

from which we can see that the refraction depends only by the index of refraction near the earth's surface. We define astronomical refraction 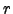$r$, to be the angular amount that the object is displaced by the refraction of the Earth's atmosphere :

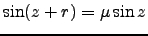$$\sin (z + r) = \mu \sin z$$ (1.13)

in cases where 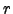$r$ is small (pretty much always) it is :

$$r = (\mu - 1) \tan z\equiv R \tan z$$ (1.14)

where we have defined 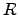$R$, known as the ``constant of refraction''. A typical value of the index of refraction is 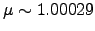$\mu \sim 1.00029$, which gives 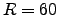$R=60$arcsec (red light). The direction of refraction is that a star apparently moves towards the zenith. Consequently in most cases, star moves in both RA and DEC:

$$r_\alpha = r \sin q$$

$$r_\delta = r \cos q$$

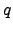where $q$ is the parallactic angle, the angle between N and the zenith :

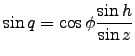$$\sin q = \cos \phi \frac{\sin h}{\sin z}$$ (1.15)

Note that the expression for 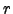$r$ is only accurate for small zenith distances (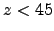$z<45$). At larger 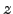$z$, we can't use the approximation of a plane parallel atmosphere. Observers have empirically found that :

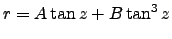$$r = A \tan z + B \tan^3 z$$ (1.16)

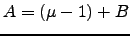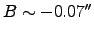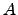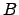where $A = (\mu-1) + B$ and $B \sim -0.07''$. But these vary with time, so for precise measurements, $A$ and $B$ must be calculated each night of observations. Of course, the index of refraction varies with wavelength, so consequently does the astronomical refraction, this gives rise to the phenomenon of atmospheric dispersion, or differential refraction. Because of the variation of index of refraction with wavelenth, every object actually appears as a little spectrum with the blue end towards the zenith. The spread in object position is proportional to 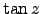$\tan z$. Note the importance of this effect for spectroscopy, and the consequent importance of the relation between a slit orientation and the parallactic angle.