



Next: Atmospheric refraction
Up: Air Mass - Extinction
Previous: Air Mass - Extinction
Index
Toward the end of his monumental work on Celestial Mechanics, Laplace has a long chapter dealing with atmospheric refraction. In the course of it, he derives a remarkable result, which seems to have been forgotten by most people today :the extinction of the atmosphere is related to its refraction. This concluson is called Laplace's extinction theorem. Exactly it sais that the logarithm of the intensity of light, of any star, is proportional to its refraction, divided by the cosine of its apparent altitude. We must immediately notice that the proportionality constant is negative, because the stars become dimmer as they approach the horizon, and their refractions increase. Furthermore, one should strictly say the relation is a linear one, rather than a simple proportionality. So we have the equation :
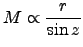 |
(1.4) |
where 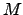 is the air mass
is the air mass 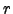 is the refraction and
is the refraction and 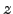 is the zenith angle. Let's see how this equation is derived.
is the zenith angle. Let's see how this equation is derived.
The differential of airmass is 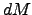 it is just proportional to the differential of path length
it is just proportional to the differential of path length 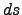 in figure 1.2, multiplied by the local density,
in figure 1.2, multiplied by the local density, 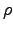
Figure 1.2:
Calculation of Laplace's theorem
|
|
Let's regard the differential of refraction from a different point of view: 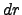 must be equal to the ray curvature multiplied by the element of path length
must be equal to the ray curvature multiplied by the element of path length 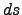 . The curvature in turn, is proportional to the component of the atmospheric density gradient
. The curvature in turn, is proportional to the component of the atmospheric density gradient 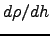 normal to the path of the ray. As the atmospheric model is horizontally stratified, its density gradient is a vector directed vertically i.e., toward the zenith. The component of this gradient normal to the ray is just proportional to
normal to the path of the ray. As the atmospheric model is horizontally stratified, its density gradient is a vector directed vertically i.e., toward the zenith. The component of this gradient normal to the ray is just proportional to 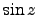 . So we have :
. So we have :
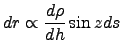 |
(1.5) |
Now we need to assume that the density gradient is proportional to the density itself. Very near the horizon, the diminution of light depends, like the refraction, upon the constitution of the atmosphere. We may, without fear of any sensible error, use the hypothesis of a uniform temperature. So we assume an exponential atmosphere, in which
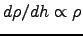 , and have :
, and have :
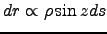 |
(1.6) |
But also we have
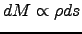 . If we eliminate the product
. If we eliminate the product 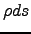 on the right side of the last proportionality for
on the right side of the last proportionality for 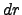 by replacing it with
by replacing it with 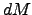 , we see that :
, we see that :
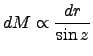 |
(1.7) |
Then integration will give Laplace's result,
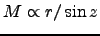 , provided that we can factor some mean value of
, provided that we can factor some mean value of 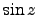 out of the integrand when we integrate this differential relation. In fact, this is not a bad approximation, because
out of the integrand when we integrate this differential relation. In fact, this is not a bad approximation, because 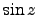 is nearly constant through the atmosphere near the zenith (where
is nearly constant through the atmosphere near the zenith (where 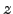 is nearly constant along the line of sight) and
is nearly constant along the line of sight) and 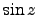 is itself nearly constant near the horizon, because the sine function flattens out near unity when
is itself nearly constant near the horizon, because the sine function flattens out near unity when 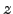 is near
is near 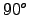 .
.
Notice that Laplace's result is trivially true for the flat-Earth approximation, where 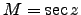 and
and
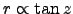 . Also, in a long duct, where the ray simply follows the curve of the Earth, and
. Also, in a long duct, where the ray simply follows the curve of the Earth, and 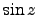 is unity, the refraction in the duct is obviously proportional to the path length there.
is unity, the refraction in the duct is obviously proportional to the path length there.




Next: Atmospheric refraction
Up: Air Mass - Extinction
Previous: Air Mass - Extinction
Index
![]() it is just proportional to the differential of path length
it is just proportional to the differential of path length ![]() in figure 1.2, multiplied by the local density,
in figure 1.2, multiplied by the local density, ![]()
![]() and
and
![]() . Also, in a long duct, where the ray simply follows the curve of the Earth, and
. Also, in a long duct, where the ray simply follows the curve of the Earth, and ![]() is unity, the refraction in the duct is obviously proportional to the path length there.
is unity, the refraction in the duct is obviously proportional to the path length there.