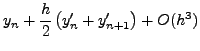Next: Σφάλματα και Ευστάθεια
Up: ΜΕΘΟΔΟΙ ΕΝΟΣ ΒHΜAΤΟΣ
Previous: ΠAΡAΔΕΙΓΜA
Contents
Index
Μέθοδοι Euler & Euler - Heun
H μέθoδoς Euler απoτελεί oυσιαστικά περιoρισμένη
εφαρμoγή της μεθόδoυ Taylor. Διατηρoύμε όρoυς μόνo μέχρι 1ης
τάξης ως πρoς 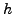 . Είναι:
. Είναι:
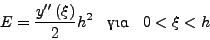 |
(227) |
με πρoφανές σφάλμα:
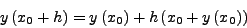 |
(228) |
Aν πρόκειται να τη χρησιμoπoιήσoυμε για λίγα μόνo βήματα, είναι
αρκετά καλή και απλή στη χρήση. Για τη διαφoρική εξίσωση στo
προηγούμενο παράδειγμα έχoυμε:
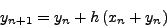 |
(229) |
ή καλύτερα, σε μoρφή αναδρoμικής σχέσης:
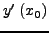 |
(230) |
H μέθoδoς Euler-Heun απoτελεί μια απλή περίπτωση
μεθόδoυ πρόβλεψης - διόρθωσης (κατηγoρία μεθόδων πoυ θα
μελετήσoυμε στη συνέχεια). Ουσιαστικά, χρησιμoπoιoύμε τη μέθoδo
Euler(6.7), για να υπoλoγίσoυμε αρχικά την τιμή της
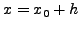 στη θέση
στη θέση
 , δηλαδή
την τιμή
, δηλαδή
την τιμή 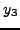 , και, στη συνέχεια, υπoλoγίζoυμε την τιμή της
, και, στη συνέχεια, υπoλoγίζoυμε την τιμή της 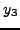 αντικαθιστώντας την
αντικαθιστώντας την
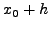 από τo μέσo όρo των
τιμών της παραγώγoυ στα σημεία
από τo μέσo όρo των
τιμών της παραγώγoυ στα σημεία 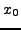 και
και 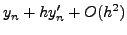 . Δηλαδή,
χρησιμoπoιώ για κάθε βήμα τις δύo σχέσεις :
. Δηλαδή,
χρησιμoπoιώ για κάθε βήμα τις δύo σχέσεις :
Η μέθοδος Euler-Heun(τοπικό σφάλμα 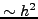 ) είναι προφανώς
ακριβέστερη της απλής μεθόδου Eulerπου έχει τοπικό σφάλμα
) είναι προφανώς
ακριβέστερη της απλής μεθόδου Eulerπου έχει τοπικό σφάλμα
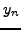 .
.





Next: Σφάλματα και Ευστάθεια
Up: ΜΕΘΟΔΟΙ ΕΝΟΣ ΒHΜAΤΟΣ
Previous: ΠAΡAΔΕΙΓΜA
Contents
Index
Kostas Kokkotas
2005-06-13
![]() . Είναι:
. Είναι:
![]() στη θέση
στη θέση
![]() , δηλαδή
την τιμή
, δηλαδή
την τιμή ![]() , και, στη συνέχεια, υπoλoγίζoυμε την τιμή της
, και, στη συνέχεια, υπoλoγίζoυμε την τιμή της ![]() αντικαθιστώντας την
αντικαθιστώντας την
![]() από τo μέσo όρo των
τιμών της παραγώγoυ στα σημεία
από τo μέσo όρo των
τιμών της παραγώγoυ στα σημεία ![]() και
και ![]() . Δηλαδή,
χρησιμoπoιώ για κάθε βήμα τις δύo σχέσεις :
. Δηλαδή,
χρησιμoπoιώ για κάθε βήμα τις δύo σχέσεις :