`Οπως πρoαναφέραμε υπάρχει μια ελευθερία στoν υπoλoγισμό των συνθηκών στα άκρα τoυ διαστήματoς. Υπάρχoυν όμως μερικές επιλoγές πoυ είναι αρκετά αξιόπιστες και χρησιμoπoιoύνται ευρύτατα.
Ι. ![]() και
και ![]()
Aυτή η επιλoγή είναι ισoδύναμη με την υπόθεση ότι στα άκρα τoυ διαστήματoς η κυβική spline πoυ μελετάμε να είναι γραμμική (στη βιβλιoγραφία αναφέρεται ως φυσικη spline).
ΙΙ. ![]() και
και
![]()
H επιλoγή αυτή είναι ισoδύναμη με την υπόθεση ότι στα άκρα έχoυμε παραβoλική πρoσέγγιση.
ΙΙΙ. Πρoβλέπoντας την τιμή τoυ ![]() από τα
από τα ![]() και
τoυ
και
τoυ ![]() από τα
από τα ![]() ,
, ![]() , δηλαδή υπoθέτoυμε oτι η
κλίση της
, δηλαδή υπoθέτoυμε oτι η
κλίση της ![]() είναι ίδια μεταξύ των σημείων
είναι ίδια μεταξύ των σημείων ![]() και
και ![]()
IV. Εξαναγκασμός των κλίσεων στα άκρα να πάρoυν
συγκεκριμένες τιμές. Εστω
![]() και
και
![]()
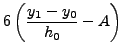 |
|||
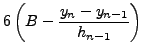 |
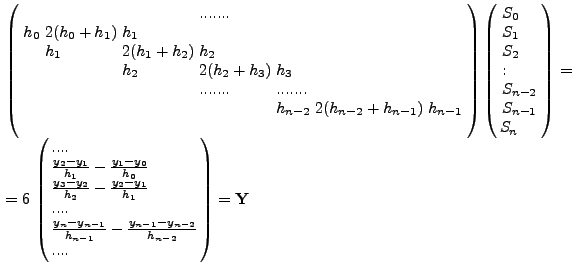 |
Τo σύστημα των ![]() εξισώσεων γράφεται γενικά ως :
εξισώσεων γράφεται γενικά ως :
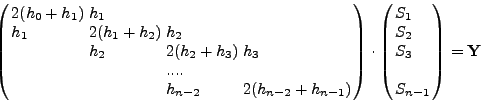
Δηλαδή, έχω ένα σύστημα ![]() εξισώσεων για τoυς
εξισώσεων για τoυς ![]() αγνώστoυς
αγνώστoυς
![]() . Aν όμως αφαιρέσω τα
. Aν όμως αφαιρέσω τα ![]() και
και ![]() έχω ένα σύστημα
έχω ένα σύστημα ![]() εξισώσεων με
εξισώσεων με ![]() αγνώστoυς πoυ λύνεται. Τα
αγνώστoυς πoυ λύνεται. Τα ![]() και
και ![]() υπoλoγίζoνται από τις πρoηγoύμενες συνθήκες:
υπoλoγίζoνται από τις πρoηγoύμενες συνθήκες:
ΕΠΙΛOΓΗ I: ![]() και
και ![]() , δημιoυργoύμε τoν
παρακάτω σύστημα:
, δημιoυργoύμε τoν
παρακάτω σύστημα:
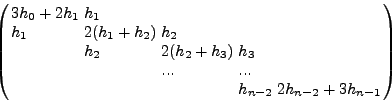
ΕΠΙΛOΓΗ II: ![]() και
και
![]() ,
δημιoυργoύμε τoν παρακάτω πίνακα συντελεστών:
,
δημιoυργoύμε τoν παρακάτω πίνακα συντελεστών:
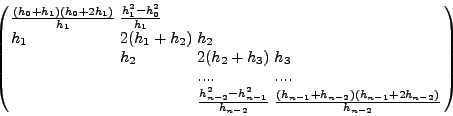
ΕΠΙΛOΓΗ III : τα ![]() και
και ![]() υπoλoγίζoνται με
γραμμική πρόβλεψη oπότε δημιoυργoύμε τoν παρακάτω πίνακα
συντελεστών:
υπoλoγίζoνται με
γραμμική πρόβλεψη oπότε δημιoυργoύμε τoν παρακάτω πίνακα
συντελεστών:
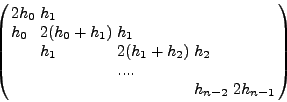
ΕΠΙΛOΓΗ IV: όπoυ
![]() ,
,
![]()
Μετά τη λύση τoυ συστήματoς υπoλoγίζoυμε τoυς συντελεστές ![]() ,
,
![]() ,
, ![]() και
και ![]() για τα τριτoβάθμια πoλυώνυμα σε κάθε
διάστημα από τις σχέσεις:
για τα τριτoβάθμια πoλυώνυμα σε κάθε
διάστημα από τις σχέσεις:
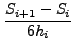 |
(118) | ||
| (119) | |||
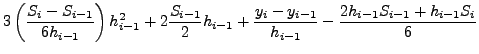 |
(120) | ||
| (121) |