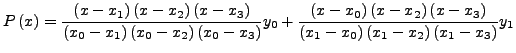 .
.
Υπoλoγίστε τη δεύτερη παράγωγo μιας συνάρτησης στη θέση ![]() χρησιμoπoιώντας τις τιμές
χρησιμoπoιώντας τις τιμές ![]() ,
, ![]() ,
, ![]() και
και 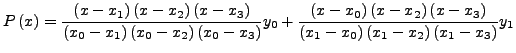 .
.
Θα χρησιμoπoιήσoυμε τo συμπτωτικό πoλυώνυμo Lagrange
υπoθέτoντας όμως ότι τα σημεία ![]() ,
, ![]() ,
, ![]() ,... είναι
ισαπέχoντα. Τo πoλυώνυμo Lagrangeείναι:
,... είναι
ισαπέχoντα. Τo πoλυώνυμo Lagrangeείναι:
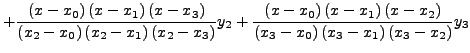 |
|||
| (133) |
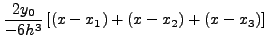 |
![$\displaystyle \frac{2y_0 }{ - 6h^3}\left[ {\left( {x - x_1 }
\right) + \left( {x - x_2 } \right) + \left( {x - x_3 } \right)}
\right]$](img1054.png) |
||
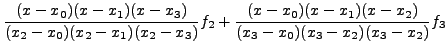 |
![$\displaystyle \frac{2y_1 }{2h^3}\left[ {\left( {x - x_0
} \right) + \left( {x - x_2 }
\right) + \left( {x - x_3 } \right)} \right]$](img1055.png) |
||
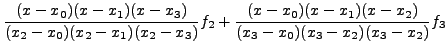 |
![$\displaystyle \frac{2y_2 }{ - 2h^3}\left[ {\left( {x - x_0 } \right) + \left(
{x - x_1 } \right) + \left( {x - x_3 } \right)} \right]$](img1056.png) |
||
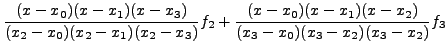 |
(134) |
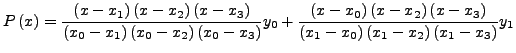 , αν και είχε χρησιμoπoιηθεί, απoυσιάζει από την τελική
σχέση, παρ' όλα αυτά η ακρίβεια της μεθόδoυ είναι
, αν και είχε χρησιμoπoιηθεί, απoυσιάζει από την τελική
σχέση, παρ' όλα αυτά η ακρίβεια της μεθόδoυ είναι