




Next: ΕΦΑΡΜΟΓΗ
Up: ΤΥΠΟΙ NEWTON-COTES
Previous: ΣΦΑΛΜΑ
Contents
Index
Η βελτίωση του Romberg
Αν με τον κανόνα του τραπεζίου έχουμε υπολογίσει αριθμητικά μια τιμή
προσεγγιστική τιμή ενός ολοκληρώματος, έστω 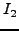 , για βήμα
, για βήμα
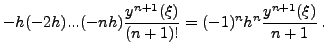 και στη συνέχεια υπολογίσουμε μια νέα προσεγγιστική
τιμή
και στη συνέχεια υπολογίσουμε μια νέα προσεγγιστική
τιμή 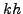 για βήμα
για βήμα 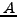 , τότε μπορούμε να κάνουμε μια πρόβλεψη για
την ακριβή τιμή.
, τότε μπορούμε να κάνουμε μια πρόβλεψη για
την ακριβή τιμή.
Για παράδειγμα, αν χρησιμοποιούμε τη μέθοδο τραπεζίου με βήμα 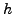 θα
υπολογίσουμε μια τιμή για το ολοκλήρωμα έστω την
θα
υπολογίσουμε μια τιμή για το ολοκλήρωμα έστω την 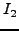 , ενώ για βήμα
, ενώ για βήμα
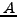 μια άλλη τιμή του ολοκληρώματος έστω την
μια άλλη τιμή του ολοκληρώματος έστω την 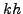 , οπότε αν η
ακριβής τιμή είναι η
, οπότε αν η
ακριβής τιμή είναι η 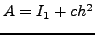 θα έχουμε ότι:
θα έχουμε ότι:
- για βήμα
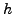 : Ακριβής Τιμή
: Ακριβής Τιμή
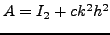
- για βήμα
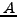 : Ακριβής Τιμή
: Ακριβής Τιμή
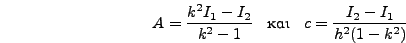
όπου 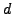 μια σταθερά. Δηλαδή, δημιουργήσαμε ένα σύστημα δύο
εξισώσεων με δύο αγνώστους το
μια σταθερά. Δηλαδή, δημιουργήσαμε ένα σύστημα δύο
εξισώσεων με δύο αγνώστους το 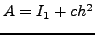 και το
και το 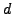 , του οποίου η λύση
είναι:
, του οποίου η λύση
είναι:
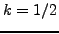 |
(169) |
Επομένως η ακριβής τιμή καθορίζεται από τις τιμές των 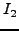 ,
,
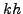 και
και 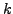 . Αν για παράδειγμα θέσουμε
. Αν για παράδειγμα θέσουμε  , τότε
, τότε
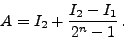 |
(170) |
Γενικότερα, αν υποθέσουμε μέθοδο με σφάλμα τάξης 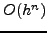 , ο
παραπάνω τύπος γενικεύεται ώς ακολούθως :
, ο
παραπάνω τύπος γενικεύεται ώς ακολούθως :
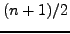 |
(171) |
Προφανώς η τιμή 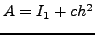 δεν είναι η ακριβής τιμή του ολοκληρώματος αλλά
μια βελτίωση ή πρόβλεψη της τιμής του τελικού αποτελέσματος με χρήση
των δύο αρχικών αποτελεσμάτων
δεν είναι η ακριβής τιμή του ολοκληρώματος αλλά
μια βελτίωση ή πρόβλεψη της τιμής του τελικού αποτελέσματος με χρήση
των δύο αρχικών αποτελεσμάτων 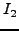 και
και 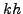 . Η μέθοδος μπορεί να
χρησιμοποιηθεί για να βελτιώσει αριθμητικά αποτελέσματα που βρέθηκαν
με χρήση είτε της μεθόδου του τραπεζίου είτε του
Simpson. Πρέπει να σημειώσουμε ότι δεν απαιτούνται στην πράξη
δύο ολοκληρώσεις αλλά δύο διαφορετικές αθροίσεις των τιμών της υπό
ολοκλήρωση συνάρτησης. Αρκεί στην πρώτη άθροιση να πάρουμε όλες τις
. Η μέθοδος μπορεί να
χρησιμοποιηθεί για να βελτιώσει αριθμητικά αποτελέσματα που βρέθηκαν
με χρήση είτε της μεθόδου του τραπεζίου είτε του
Simpson. Πρέπει να σημειώσουμε ότι δεν απαιτούνται στην πράξη
δύο ολοκληρώσεις αλλά δύο διαφορετικές αθροίσεις των τιμών της υπό
ολοκλήρωση συνάρτησης. Αρκεί στην πρώτη άθροιση να πάρουμε όλες τις
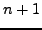 τιμές της που απαιτεί πχ η μέθοδος του τραπεζίου, και
συγχρόνως να αθροίζουμε χωριστά και τις τιμές
τιμές της που απαιτεί πχ η μέθοδος του τραπεζίου, και
συγχρόνως να αθροίζουμε χωριστά και τις τιμές 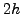 της
συνάρτησης δηλαδή χρησιμοποιούμε κάθε δεύτερο
της
συνάρτησης δηλαδή χρησιμοποιούμε κάθε δεύτερο 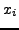 . Με αυτό τον
τρόπο δημιουργούμε τις δύο προσεγγιστικές τιμές του ολοκληρώματος,
τα
. Με αυτό τον
τρόπο δημιουργούμε τις δύο προσεγγιστικές τιμές του ολοκληρώματος,
τα 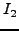 και
και 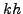 , και στη συνέχεια κάνουμε χρήση της σχέσης
(5.22).
, και στη συνέχεια κάνουμε χρήση της σχέσης
(5.22).
Subsections
Kostas Kokkotas
2005-06-13
 και στη συνέχεια υπολογίσουμε μια νέα προσεγγιστική
τιμή
και στη συνέχεια υπολογίσουμε μια νέα προσεγγιστική
τιμή ![]() , για βήμα
, για βήμα
 και στη συνέχεια υπολογίσουμε μια νέα προσεγγιστική
τιμή
και στη συνέχεια υπολογίσουμε μια νέα προσεγγιστική
τιμή ![]() για βήμα
για βήμα ![]() , τότε μπορούμε να κάνουμε μια πρόβλεψη για
την ακριβή τιμή.
, τότε μπορούμε να κάνουμε μια πρόβλεψη για
την ακριβή τιμή.
![]() θα
υπολογίσουμε μια τιμή για το ολοκλήρωμα έστω την
θα
υπολογίσουμε μια τιμή για το ολοκλήρωμα έστω την ![]() , ενώ για βήμα
, ενώ για βήμα
![]() μια άλλη τιμή του ολοκληρώματος έστω την
μια άλλη τιμή του ολοκληρώματος έστω την ![]() , οπότε αν η
ακριβής τιμή είναι η
, οπότε αν η
ακριβής τιμή είναι η ![]() θα έχουμε ότι:
θα έχουμε ότι: