




Next: ΚΡΙΤΙΚΗ
Up: ΤΥΠΟΙ NEWTON-COTES
Previous: ΕΦΑΡΜΟΓΗ
Contents
Index
Εφαρμογή των Splinesστην Παραγώγιση και Ολοκλήρωση συναρτήσεων
Η προσέγγιση με splinesαποτελεί μια εξαιρετική μέθοδο
προσέγγισης μιας συνάρτησης ή ένος συνόλου 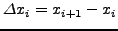 διακριτών
δεδομένων με 3ο-βάθμια πολυώνυμα. Αν επομένως για ένα σύνολο
διακριτών δεδομένων
διακριτών
δεδομένων με 3ο-βάθμια πολυώνυμα. Αν επομένως για ένα σύνολο
διακριτών δεδομένων 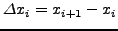 έχουμε υπολογίσει τους συντελεστές
των 3ο-βαθμίων πολυωνύμων τότε οι splinesμπορούν να
χρησιμοποιηθούν για τον αριθμητικό υπολογισμό παραγώγων και
ολοκληρωμάτων. Η κυβική splineπου προσεγγίζει μια συνάρτηση
σε ένα διάστημα
έχουμε υπολογίσει τους συντελεστές
των 3ο-βαθμίων πολυωνύμων τότε οι splinesμπορούν να
χρησιμοποιηθούν για τον αριθμητικό υπολογισμό παραγώγων και
ολοκληρωμάτων. Η κυβική splineπου προσεγγίζει μια συνάρτηση
σε ένα διάστημα
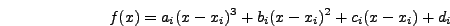 γράφεται:
γράφεται:
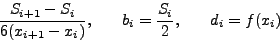 |
(172) |
και οι συντελεστές 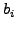 ,
, 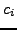 ,
, 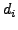 και
και 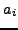 δίνονται από τις
σχέσεις :
δίνονται από τις
σχέσεις :
Ετσι, η πρώτη και η δεύτερη παράγωγος σε κάποιο τυχαίο σημείο
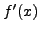 υπολογίζονται αυτόματα από την παραγώγιση του 3ο-βάθμιου
πολυωνύμου (5.23). Δηλαδή, από τις σχέσεις
υπολογίζονται αυτόματα από την παραγώγιση του 3ο-βάθμιου
πολυωνύμου (5.23). Δηλαδή, από τις σχέσεις
Ενώ στα 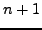 σημεία
σημεία 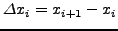 οι παράγωγοι δίνονται πολύ απλά ως
οι παράγωγοι δίνονται πολύ απλά ως
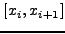 |
(176) |
Είναι προφανές ότι η κυβική splineδίνει ικανοποιητικά
αποτελέσματα μόνο για τον υπολογισμό παραγώγων πρώτης και δεύτερης
τάξης. Ενώ για ανώτερης τάξης παραγώγους απαιτούνται ανώτερης τάξης
splines.
Η αριθμητική ολοκλήρωση μιας συνάρτησης 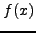 ή μιας
ή μιας 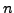 -άδας
σημείων
-άδας
σημείων 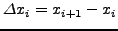 μπορεί να προσεγγιστεί με αντικατάσταση της
συνάρτησης με το 3ο-βάθμιο πολυώνυμο σε κάθε διάστημα
μπορεί να προσεγγιστεί με αντικατάσταση της
συνάρτησης με το 3ο-βάθμιο πολυώνυμο σε κάθε διάστημα
![$[x_i,x_{i+1}]$](img1202.png) , δηλαδή:
, δηλαδή:
Στην πράξη χρησημοποιούμε ισαπέχοντα σημεία οπότε αν
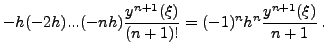 , τότε η ολοκλήρωση ανάγεται στον υπολογισμό των
αθροισμάτων των συντελεστών της κυβικής spline. Δηλαδή,
, τότε η ολοκλήρωση ανάγεται στον υπολογισμό των
αθροισμάτων των συντελεστών της κυβικής spline. Δηλαδή,
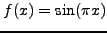 |
(177) |
Eπομένως, αρκεί ο υπολογισμός των παραπάνω αθροισμάτων για να έχουμε
μια εξαιρετικά ακριβή τιμή του ολοκληρώματος.
Subsections





Next: ΚΡΙΤΙΚΗ
Up: ΤΥΠΟΙ NEWTON-COTES
Previous: ΕΦΑΡΜΟΓΗ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() διακριτών
δεδομένων με 3ο-βάθμια πολυώνυμα. Αν επομένως για ένα σύνολο
διακριτών δεδομένων
διακριτών
δεδομένων με 3ο-βάθμια πολυώνυμα. Αν επομένως για ένα σύνολο
διακριτών δεδομένων ![]() έχουμε υπολογίσει τους συντελεστές
των 3ο-βαθμίων πολυωνύμων τότε οι splinesμπορούν να
χρησιμοποιηθούν για τον αριθμητικό υπολογισμό παραγώγων και
ολοκληρωμάτων. Η κυβική splineπου προσεγγίζει μια συνάρτηση
σε ένα διάστημα
έχουμε υπολογίσει τους συντελεστές
των 3ο-βαθμίων πολυωνύμων τότε οι splinesμπορούν να
χρησιμοποιηθούν για τον αριθμητικό υπολογισμό παραγώγων και
ολοκληρωμάτων. Η κυβική splineπου προσεγγίζει μια συνάρτηση
σε ένα διάστημα
![]() γράφεται:
γράφεται:
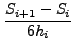
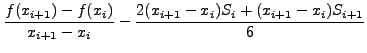
![]() ή μιας
ή μιας ![]() -άδας
σημείων
-άδας
σημείων ![]() μπορεί να προσεγγιστεί με αντικατάσταση της
συνάρτησης με το 3ο-βάθμιο πολυώνυμο σε κάθε διάστημα
μπορεί να προσεγγιστεί με αντικατάσταση της
συνάρτησης με το 3ο-βάθμιο πολυώνυμο σε κάθε διάστημα
![$[x_i,x_{i+1}]$](img1202.png) , δηλαδή:
, δηλαδή:
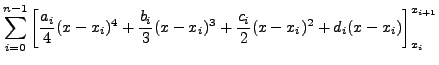
![$\displaystyle \sum_{i=0}^{n-1}
\left[\frac{a_i}{4}(x-x_i)^4 +\frac{b_i}{3}(x-x_i)^3
+\frac{c_i}{2}(x-x_i)^2 +d_i(x-x_i)\right]_{x_i}^{x_{i+1}}$](img1204.png)
![$\displaystyle \sum_{i=0}^{n-1} \left[\frac{a_i}{4}(x_{i+1}-x_i)^4 +
\frac{b_i}{3}(x_{i+1}-x_i)^3 + \frac{c_i}{2}(x_{i+1}-x_i)^2 +
d_i(x_{i+1}-x_i)\right] \, .$](img1205.png)
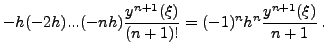 , τότε η ολοκλήρωση ανάγεται στον υπολογισμό των
αθροισμάτων των συντελεστών της κυβικής spline. Δηλαδή,
, τότε η ολοκλήρωση ανάγεται στον υπολογισμό των
αθροισμάτων των συντελεστών της κυβικής spline. Δηλαδή,