




Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΜΕΘΟΔΟΣ GAUSS
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Η μέθοδος Gaussμπορεί να γενικευθεί για αναπτύγματα
περισσοτέρων όρων. Δηλαδή, αν χρησιμοποιήσουμε για 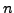 σημεία θα
έχουμε μια σχέση της μορφής :
σημεία θα
έχουμε μια σχέση της μορφής :
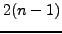 |
(201) |
Με αυτό τον τρόπο θα πρέπει να λυθεί ένα σύστημα 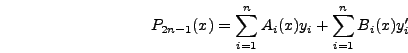 εξισώσεων για
τον υπολογισμό των
εξισώσεων για
τον υπολογισμό των 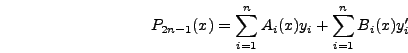 ποσοτήτων
ποσοτήτων 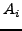 και
και 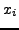 . Η μέθοδος με
βάση τα παραπάνω θα είνα ακριβής για πολυώνυμα έως και βαθμού
. Η μέθοδος με
βάση τα παραπάνω θα είνα ακριβής για πολυώνυμα έως και βαθμού
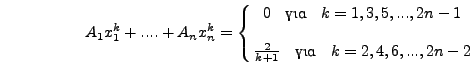 , οπότε οι
, οπότε οι 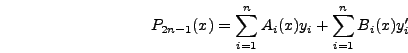 εξισώσεις αποδεικνύεται ότι μπορούν να
γραφούν συνοπτικά ώς :
εξισώσεις αποδεικνύεται ότι μπορούν να
γραφούν συνοπτικά ώς :
 |
(202) |
Αποδεικνύεται ότι τα 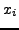 είναι ρίζες των πολυωνύμων Legendre
βαθμού
είναι ρίζες των πολυωνύμων Legendre
βαθμού 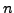 των οποίων οι ρίζες βρίσκονται πάντα εντός του
διαστήματος
των οποίων οι ρίζες βρίσκονται πάντα εντός του
διαστήματος  . Τα πολυώνυμα Legendreδημιουργούνται από
την αναδρομική σχέση:
. Τα πολυώνυμα Legendreδημιουργούνται από
την αναδρομική σχέση:
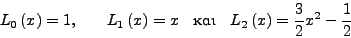 |
(203) |
όπου τα 3 πρώτα πολυώνυμα είναι:
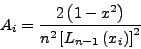 |
(204) |
Κατ' αναλογία τα 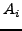 δίνονται από τις σχέσεις:
δίνονται από τις σχέσεις:
![\begin{displaymath}
A_i = \frac{{2\left( {1 - x^2 } \right)}}{{n^2 \left[ {L_{n - 1}
\left( {x_i } \right)} \right]^2 }}
\end{displaymath}](img1297.png) |
(205) |
Για παράδειγμα αν 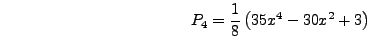 θα πρέπει να βρούμε τις ρίζες του 4ο-βάθμιου
πολυωνύμου Legendre
θα πρέπει να βρούμε τις ρίζες του 4ο-βάθμιου
πολυωνύμου Legendre
που είναι
![$x_i=\pm\left[(15\pm2\sqrt{30})/35\right]^{1/2}$](img1300.png) και στη συνέχεια
χρησιμοποιώντας τη σχέση (5.56) υπολογίζω τα
και στη συνέχεια
χρησιμοποιώντας τη σχέση (5.56) υπολογίζω τα 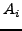 . Οι
ακριβείς τιμές τους δίνονται στον Πίνακα 5.4.
. Οι
ακριβείς τιμές τους δίνονται στον Πίνακα 5.4.
Επομένως, αρκεί να υπολογισθούν μια φορά τα 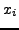 και
και 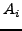 για
διάφορους αριθμούς σημείων και στη συνέχεια χρησιμοποιούνται σε κάθε
πρόβλημα.
για
διάφορους αριθμούς σημείων και στη συνέχεια χρησιμοποιούνται σε κάθε
πρόβλημα.
Table:
Οι τιμές των 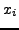 και
και 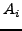 της μεθόδου
Gauss-Legendreγια 2, 4 και 8 σημεία.
της μεθόδου
Gauss-Legendreγια 2, 4 και 8 σημεία.
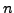 |
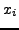 |
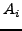 |
| 2 |
 0.57735027 0.57735027 |
1.0000000 |
| 4 |
 0.86113631 0.86113631 |
0.34785485 |
| |
 0.33948104 0.33948104 |
0.62214515 |
| 8 |
 0.96028986 0.96028986 |
0.10122854 |
| |
 0.79666648 0.79666648 |
0.22381034 |
| |
 0.52553241 0.52553241 |
0.31370665 |
| |
 0.18343464 0.18343464 |
0.36268378 |
|
Subsections





Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΜΕΘΟΔΟΣ GAUSS
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() σημεία θα
έχουμε μια σχέση της μορφής :
σημεία θα
έχουμε μια σχέση της μορφής :
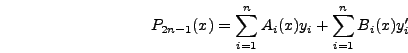 εξισώσεων για
τον υπολογισμό των
εξισώσεων για
τον υπολογισμό των 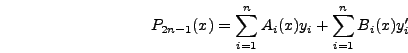 ποσοτήτων
ποσοτήτων 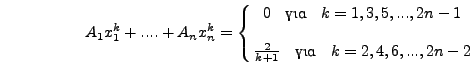 , οπότε οι
, οπότε οι 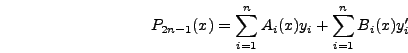 εξισώσεις αποδεικνύεται ότι μπορούν να
γραφούν συνοπτικά ώς :
εξισώσεις αποδεικνύεται ότι μπορούν να
γραφούν συνοπτικά ώς :
![]() θα πρέπει να βρούμε τις ρίζες του 4ο-βάθμιου
πολυωνύμου Legendre
θα πρέπει να βρούμε τις ρίζες του 4ο-βάθμιου
πολυωνύμου Legendre
![]() και
και ![]() για
διάφορους αριθμούς σημείων και στη συνέχεια χρησιμοποιούνται σε κάθε
πρόβλημα.
για
διάφορους αριθμούς σημείων και στη συνέχεια χρησιμοποιούνται σε κάθε
πρόβλημα.