![$[a,b]$](img1238.png) και στη συνέχεια προσπαθούσαμε να υπολογίσουμε μόνο τους
συντελεστές της συνάρτησης
και στη συνέχεια προσπαθούσαμε να υπολογίσουμε μόνο τους
συντελεστές της συνάρτησης
Στην μέθοδο των προσδιοριστέων
συντελεστών επιλέγαμε συγκεκριμένα σημεία στο διάστημα ολοκλήρωσης
![$[a,b]$](img1238.png) και στη συνέχεια προσπαθούσαμε να υπολογίσουμε μόνο τους
συντελεστές της συνάρτησης
και στη συνέχεια προσπαθούσαμε να υπολογίσουμε μόνο τους
συντελεστές της συνάρτησης ![]() σ’ αυτά τα σημεία. Αν τώρα
επεκτείνουμε την τεχνική και ζητήσουμε και τον υπολογισμό όχι μόνο
των συντελεστών αλλά και συγκεκριμένων σημείων
σ’ αυτά τα σημεία. Αν τώρα
επεκτείνουμε την τεχνική και ζητήσουμε και τον υπολογισμό όχι μόνο
των συντελεστών αλλά και συγκεκριμένων σημείων
![]() εντός του διαστήματος ολοκλήρωσης τότε αναγόμαστε σε μια εξαιρετική
μέθοδο αριθμητικής ολοκλήρωσης γνωστή ως η μέθοδος του
Gauss.
εντός του διαστήματος ολοκλήρωσης τότε αναγόμαστε σε μια εξαιρετική
μέθοδο αριθμητικής ολοκλήρωσης γνωστή ως η μέθοδος του
Gauss.
Στη συνέχεια θα εξετάσου μια απλή περίπτωση εφαρμογής της μεθόδου,
`Εστω ότι το διαστημα ολοκλήρωσης είναι το ![]() τότε υποθέτουμε
ότι :
τότε υποθέτουμε
ότι :
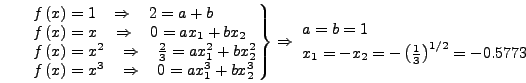 . Με αυτό τον τρόπο δημιουργούμε, αντικαθιστώντας κάθε μία
από αυτές τις συναρτήσεις στη σχέση (5.50), ένα σύστημα
τεσσάρων εξισώσεων με τέσσερις αγνώστους, δηλαδή:
. Με αυτό τον τρόπο δημιουργούμε, αντικαθιστώντας κάθε μία
από αυτές τις συναρτήσεις στη σχέση (5.50), ένα σύστημα
τεσσάρων εξισώσεων με τέσσερις αγνώστους, δηλαδή: