| (206) |
Αν ένα ολοκλήρωμα είναι της μορφής :
| (206) |
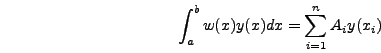 είναι μια συνάρτηση βάρους, τότε μπορούμε να
επεκτείνουμε τη μέθοδο Gaussχρησιμοποιώντας όχι μόνο τα
πολυώνυμα Legendreαλλά και άλλου είδους ορθογώνια πολυώνυμα
ανάλογα με τη μορφή της υπο ολοκλήρωση συνάρτησης. Επομένως το
παραπάνω ολοκλήρωμα θα γραφεί ως :
είναι μια συνάρτηση βάρους, τότε μπορούμε να
επεκτείνουμε τη μέθοδο Gaussχρησιμοποιώντας όχι μόνο τα
πολυώνυμα Legendreαλλά και άλλου είδους ορθογώνια πολυώνυμα
ανάλογα με τη μορφή της υπο ολοκλήρωση συνάρτησης. Επομένως το
παραπάνω ολοκλήρωμα θα γραφεί ως :
| (207) |
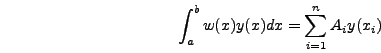 θα έχουμε τις
παρακάτω επιλογές.
θα έχουμε τις
παρακάτω επιλογές.
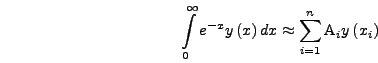 που είναι η μέθοδος της προηγούμενης ενότητας.
που είναι η μέθοδος της προηγούμενης ενότητας.
| (208) |
| (209) |
![\begin{displaymath}
A_i = \frac{(n!)^2}{x_i \left[ L'_n(x_i)\right]^2 }
\end{displaymath}](img1313.png) |
(210) |
| (211) |
| (212) |
![\begin{displaymath}
A_i=\frac{2^{n + 1} n!\sqrt{\pi}}{\left[H_n'(x_i)\right]^2 }
\end{displaymath}](img1317.png) |
(213) |
| (214) |
| (215) |
| (216) |
| (217) |
| (218) |