Next: ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Up: ΑΡΙΘΜΗΤΙΚΗ ΟΛΟΚΛΗΡΩΣΗ
Previous: Γενίκευση της μεθόδου Gauss
Contents
Index
- Να αποδειχθεί ο τύπος του σφάλματος για τη μέθοδο
Simpson 3/8(σχέση 5.12).
- Με τη μέθοδο του τραπεζίου ολοκληρώστε τις συναρτήσεις
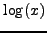 ,
, 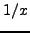 , και
, και 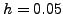 με βήμα
με βήμα 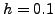 και
και 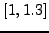 για
το διάστημα
για
το διάστημα ![$[1,1.3]$](img1327.png) . Συγκρίνετε με τα ακριβή αποτελέσματα και
επίσης πόσο μεταβάλλεται η ακρίβεια με τον υποδιπλασιασμό του
βήματος.
. Συγκρίνετε με τα ακριβή αποτελέσματα και
επίσης πόσο μεταβάλλεται η ακρίβεια με τον υποδιπλασιασμό του
βήματος.
- Στο προηγούμενο πρόβλημα εφαρμόστε τη μέθοδο Rombergκαι
εξετάστε την βελτίωση των αποτελεσμάτων.
- Επαναλάβετε, την άσκηση 1 για τη μέθοδο του Simpsonκαι
συγκρίνετε την ακρίβειά της με αυτή της μεθόδου του τραπεζίου.
- Υπολογίστε την τιμή του ολοκληρώματος
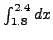 διαιρώντας το διάστημα ολοκλήρωσης σε 6 υποδιαστήματα,
χρησιμοποιώντας τον κανόναα του τραπεζίου και στη συνέχεια τον
κανόνα του Simpson. Συγκρίνετε το αποτέλεσμά σας με το ακριβές
και εξετάστε αν το σφάλμα είναι το αναμενόμενο.
διαιρώντας το διάστημα ολοκλήρωσης σε 6 υποδιαστήματα,
χρησιμοποιώντας τον κανόναα του τραπεζίου και στη συνέχεια τον
κανόνα του Simpson. Συγκρίνετε το αποτέλεσμά σας με το ακριβές
και εξετάστε αν το σφάλμα είναι το αναμενόμενο.
- Εφαρμόστε τη μέθοδο Rombergστο παραπάνω πρόβλημα.
- Εαν θέλαμε να υπολογίσουμε την τιμή του ολοκληρώματος
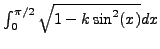 χρησιμοποιώντας τον κανόνα του τραπεζίου, και
απαιτούσαμε ακρίβεια 5 δεκαδικών ψηφίων, πόσο μικρό έπρεπε να είναι
το βήμα
χρησιμοποιώντας τον κανόνα του τραπεζίου, και
απαιτούσαμε ακρίβεια 5 δεκαδικών ψηφίων, πόσο μικρό έπρεπε να είναι
το βήμα 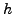 ? Υπολογίστε το θεωρητικά και στη συνέχεια εξετάστε αν
συμφωνεί με το αριθμητικό αποτέλεσμα.
? Υπολογίστε το θεωρητικά και στη συνέχεια εξετάστε αν
συμφωνεί με το αριθμητικό αποτέλεσμα.
- Επαναλάβετε το προηγούμενο πρόβλημα χρησιμοποιώντας τη μέθοδο
του Simpson.
- Υπολογίστε το ελλειπτικό ολοκλήρωμα
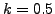 για
για  και
και 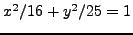 με ακρίβεια 4 δεκαδικά ψηφίων.
με ακρίβεια 4 δεκαδικά ψηφίων.
- Υπολογίστε το μήκος της περιφέρειας της έλλειψης
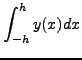 με ακρίβεια 6 δεκαδικών ψηφίων.
με ακρίβεια 6 δεκαδικών ψηφίων.
- Με τη μέθοδο των προσδιοριστέων συντελεστών υπολογίστε τους
συντελεστές στον τύπο
έτσι ώστε να είνα ακριβής για όσο το δυνατόν μεγαλύτερου βαθμού
πολυώνυμο.
- Με τη μέθοδο των προσδιοριστέων συντελεστών δείξτε ότι ισχύει
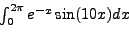 |
(220) |
για κάθε πολυώνυμο έως και 4ου βαθμού.
- Υπολογίστε με τη μέθοδο του Filonτο ολοκλήρωμα
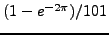 . Συγκρίνετε την ακρίβεια της
μεθόδου με την ακρίβεια της μεθόδου του Simpsonστον ίδιο
αριθμό σημείων [H αναλυτική επίλυση δίνει
. Συγκρίνετε την ακρίβεια της
μεθόδου με την ακρίβεια της μεθόδου του Simpsonστον ίδιο
αριθμό σημείων [H αναλυτική επίλυση δίνει
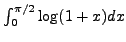 ].
].
- Εφαρμόστε τη μέθοδο Gauss-Legendreκαι κατόπιν τη μέθοδο
Simpson-Rombergγια τον υπολογισμό του ολοκληρώματος
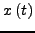 (η ακριβής τιμή είναι 0.856589940). Τι
παρατηρείτε ?
(η ακριβής τιμή είναι 0.856589940). Τι
παρατηρείτε ?
Kostas Kokkotas
2005-06-13
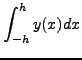 με ακρίβεια 6 δεκαδικών ψηφίων.
με ακρίβεια 6 δεκαδικών ψηφίων.
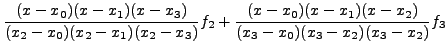
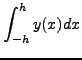 με ακρίβεια 6 δεκαδικών ψηφίων.
με ακρίβεια 6 δεκαδικών ψηφίων.