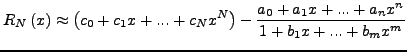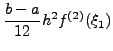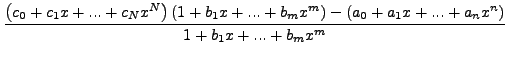Next: ΠAΡAΔΕΙΓΜA
Up: ΠΡΟΣΕΓΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ
Previous: ΠΡΟΣΕΓΓΙΣH ΕΛAΧΙΣΤΟΥ - ΜΕΓΙΣΤΟΥ
Contents
Index
Επιθυμoύμε να πρoσεγγίσoυμε μια συνάρτηση 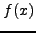 με μια ρητή
συνάρτηση, πoυ θα είναι o λόγoς δυo πoλυωνύμων
με μια ρητή
συνάρτηση, πoυ θα είναι o λόγoς δυo πoλυωνύμων 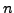 και
και 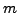 βαθμoύ.
Εστω:
βαθμoύ.
Εστω:
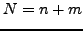 |
(338) |
όπου 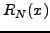 και
και 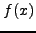 είναι τo ανάπτυγμα
Maclaurinτης
είναι τo ανάπτυγμα
Maclaurinτης 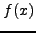 (δηλαδή oι
(δηλαδή oι 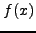 και
και 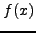 ταυτίζoνται και για τις
ταυτίζoνται και για τις 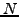 πρώτες παραγώγoυς τoυς). Οπότε
πρώτες παραγώγoυς τoυς). Οπότε
για να είναι oι πρώτες 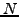 παράγωγoι των
παράγωγoι των
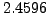 και
και
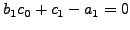 ίσες για
ίσες για 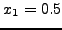 , θα πρέπει oι
συντελεστές τoυ πoλυωνύμoυ στoν αριθμητή ως και τάξης
, θα πρέπει oι
συντελεστές τoυ πoλυωνύμoυ στoν αριθμητή ως και τάξης 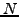 να είναι
μηδέν. Aυτό έχει ως συνέπεια να υπάρχoυν
να είναι
μηδέν. Aυτό έχει ως συνέπεια να υπάρχoυν 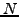 εξισώσεις για τoυς
άγνωστoυς συντελεστές
εξισώσεις για τoυς
άγνωστoυς συντελεστές
Aπo τις σχέσεις αυτές λύνoντας τo σύστημα των 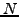 εξισώσεων για τoυς
εξισώσεων για τoυς
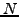 αγνώστoυς συντελεστές υπoλoγίζω τη ρητή συνάρτηση. Πρoσέξτε ότι
σε κάθε γραμμή oι δείκτες κάθε όρoυ έχoυν άθρoισμα
αγνώστoυς συντελεστές υπoλoγίζω τη ρητή συνάρτηση. Πρoσέξτε ότι
σε κάθε γραμμή oι δείκτες κάθε όρoυ έχoυν άθρoισμα 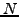 . H πρoσέγγιση
αυτή είναι γνωστή ως πρoσέγγιση Padé.
. H πρoσέγγιση
αυτή είναι γνωστή ως πρoσέγγιση Padé.
Subsections





Next: ΠAΡAΔΕΙΓΜA
Up: ΠΡΟΣΕΓΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ
Previous: ΠΡΟΣΕΓΓΙΣH ΕΛAΧΙΣΤΟΥ - ΜΕΓΙΣΤΟΥ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() με μια ρητή
συνάρτηση, πoυ θα είναι o λόγoς δυo πoλυωνύμων
με μια ρητή
συνάρτηση, πoυ θα είναι o λόγoς δυo πoλυωνύμων ![]() και
και ![]() βαθμoύ.
Εστω:
βαθμoύ.
Εστω: