




Next: Αριθμητική Λύση: Μέθοδος Crank-Nicholson
Up: ΠΑΡΑΒΟΛΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Previous: ΠΑΡΑΒΟΛΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Contents
Index
Ας υποθέσουμε ότι το διάστημα 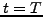 υποδιαιρείται σε
υποδιαιρείται σε 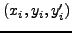 υποδιαστήματα
υποδιαστήματα 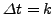 και ας υποθέσουμε ότι στη χρονική
διεύθυνση ότι θα λύσουμε τη ΔΕΜΠ έως τη χρονική στιγμή
και ας υποθέσουμε ότι στη χρονική
διεύθυνση ότι θα λύσουμε τη ΔΕΜΠ έως τη χρονική στιγμή 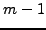 οπότε
θα θεωρήσουμε
οπότε
θα θεωρήσουμε 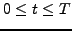 υποδιαιρέσεις στο διάστημα
υποδιαιρέσεις στο διάστημα 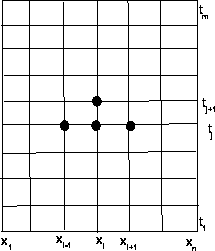 , Σχήμα
8.7.
, Σχήμα
8.7.
Figure:
Η διαμέριση(πλέγμα) για την αριθμητική επίλυση της παραβολικής εξίσωσης.
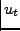 |
Αντικαθιστώντας τις μερικές παραγώγους 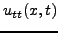 και
και 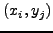 απο τις
εξισώσεις διαφορών
απο τις
εξισώσεις διαφορών
οπότε αντικαθιστούμε την εξίσωση (8.34) με την εξίσωση
διαφορών
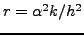 |
(379) |
οπότε αν θέσουμε
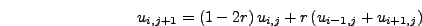 στην παραπάνω σχέση δημιουργούμε
την εξίσωση διαφορών
στην παραπάνω σχέση δημιουργούμε
την εξίσωση διαφορών
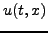 |
(380) |
Η εξίσωση αυτή δίνει τις τιμές της συνάρτησης 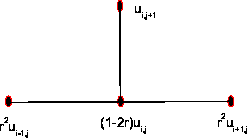 στην γραμμή
στην γραμμή
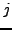 σαν συνάρτηση των τιμών της συνάρτησης στη γραμμή
σαν συνάρτηση των τιμών της συνάρτησης στη γραμμή 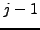 , όπως
φαίνεται στο Σχήμα 8.8.
, όπως
φαίνεται στο Σχήμα 8.8.
Figure:
Tο αριθμητικό σχήμα
για την αριθμητική επίλυση της παραβολικής εξίσωσης.
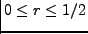 |
Το παραπάνω αριθμητικό σχήμα είναι εξαιρετικά απλό και ο
προγραμματισμός του σε οποιαδήποτε γλώσσα σχεδόν τετριμμένος. Παρ'
όλα ταύτα θα πρέπει να εξετάσουμε την ευστάθειά του, πιο
συγκεκριμένα το σχήμα είναι ευσταθές για
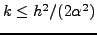 . Δηλαδή,
το χρονικό βήμα θα πρέπει να καθορίζεται από τη σχέση
. Δηλαδή,
το χρονικό βήμα θα πρέπει να καθορίζεται από τη σχέση
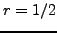 . Ειδικά η επιλογή
. Ειδικά η επιλογή  απλοποιεί το αριθμητικό
σχήμα (8.40) που γράφεται στη μορφή:
απλοποιεί το αριθμητικό
σχήμα (8.40) που γράφεται στη μορφή:
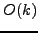 |
(381) |
Θα πρέπει να παρατηρήσουμε ότι το σχήμα που παρουσιάσαμε είναι
πρώτης τάξης, 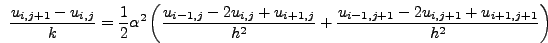 , ως προς το χρόνο και δεύτερης τάξης,
, ως προς το χρόνο και δεύτερης τάξης, 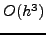 ,
ως προς το χώρο.
,
ως προς το χώρο.
Kostas Kokkotas
2005-06-13
 , Σχήμα
8.7.
, Σχήμα
8.7.
![]() υποδιαιρείται σε
υποδιαιρείται σε ![]() υποδιαστήματα
υποδιαστήματα ![]() και ας υποθέσουμε ότι στη χρονική
διεύθυνση ότι θα λύσουμε τη ΔΕΜΠ έως τη χρονική στιγμή
και ας υποθέσουμε ότι στη χρονική
διεύθυνση ότι θα λύσουμε τη ΔΕΜΠ έως τη χρονική στιγμή ![]() οπότε
θα θεωρήσουμε
οπότε
θα θεωρήσουμε ![]() υποδιαιρέσεις στο διάστημα
υποδιαιρέσεις στο διάστημα  , Σχήμα
8.7.
, Σχήμα
8.7.
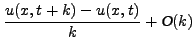
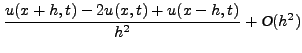
 στην γραμμή
στην γραμμή
![]() . Δηλαδή,
το χρονικό βήμα θα πρέπει να καθορίζεται από τη σχέση
. Δηλαδή,
το χρονικό βήμα θα πρέπει να καθορίζεται από τη σχέση
![]() . Ειδικά η επιλογή
. Ειδικά η επιλογή ![]() απλοποιεί το αριθμητικό
σχήμα (8.40) που γράφεται στη μορφή:
απλοποιεί το αριθμητικό
σχήμα (8.40) που γράφεται στη μορφή: