Η μέθοδος των Crankκαι Nicholsonείναι μια έμμεση μέθοδος αριθμητικής επίλυσης παραβολικών ΔΕΜΠ.
Σ' αυτήν τη μέθοδο η τιμή της συνάρτησης ![]() σε κάποιο σημείο
σε κάποιο σημείο
![]() δεν υπολογίζεται απ'ευθείας αλλά μέσω της επίλυσης ενός
γραμμικού συστήματος εξισώσεων. Πιο συγκεκριμένα στην διακριτοποίηση
της 2ης χωρικής παραγώγου της
δεν υπολογίζεται απ'ευθείας αλλά μέσω της επίλυσης ενός
γραμμικού συστήματος εξισώσεων. Πιο συγκεκριμένα στην διακριτοποίηση
της 2ης χωρικής παραγώγου της ![]() (δηλαδή της
(δηλαδή της ![]() ) αντί να
χρησιμοποιήσουμε τα στοιχεία της γραμμής
) αντί να
χρησιμοποιήσουμε τα στοιχεία της γραμμής ![]() που είνα γνωστά,
χρησιμοποιούμε και τα άγνωστα στοιχεία της γραμμής
που είνα γνωστά,
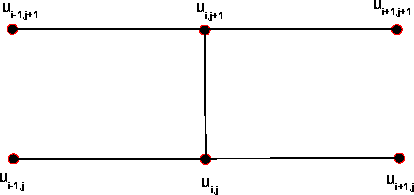
χρησιμοποιούμε και τα άγνωστα στοιχεία της γραμμής ![]() όπως
φαίνεται στο Σχήμα 8.9. Για την ακρίβεια παίρνουμε
το μέσο όρο των διακριτοποιημένων τιμών της
όπως
φαίνεται στο Σχήμα 8.9. Για την ακρίβεια παίρνουμε
το μέσο όρο των διακριτοποιημένων τιμών της ![]() όπως φαίνεται
στην παρακάτω σχέση:
όπως φαίνεται
στην παρακάτω σχέση:
| (382) |
| (383) |
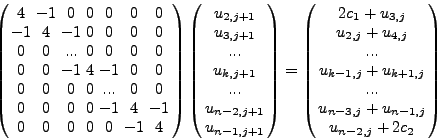 |
(384) |
 |
(385) |
Προφανώς, η διαδικασία αυτή είναι σημαντικά πιο χρονοβόρα από αυτήν
που παρουσιάσαμε στην προηγούμενη ενότητα, αλλά είναι ευστάθης
για κάθε τιμή, του ![]() . Υπενθυμίζουμε, ότι στην προηγούμενη μέθοδο
το κριτήριο ευστάθειας επέτρεπε τιμές
. Υπενθυμίζουμε, ότι στην προηγούμενη μέθοδο
το κριτήριο ευστάθειας επέτρεπε τιμές ![]() . Αρα με την
έμμεση μέθοδο των Crank-Nicholsonμπορούμε να χρησιμοποιήσουμε
σημαντικά μεγαλύτερο χρονικό βήμα που επιταχύνει σημαντικά την
επίλυση του προβλήματος.
. Αρα με την
έμμεση μέθοδο των Crank-Nicholsonμπορούμε να χρησιμοποιήσουμε
σημαντικά μεγαλύτερο χρονικό βήμα που επιταχύνει σημαντικά την
επίλυση του προβλήματος.