




Next: ΣΥΣΤHΜAΤA ΜH-ΓΡAΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Up: Δεύτερης τάξης Newton-Raphson (Halley)
Previous: ΣΥΓΚΛΙΣΗ
Contents
Index
Να αποδείξετε ότι η τετραγωνική ρίζα ενός αριθμού 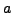 δίνεται
από τη σχέση:
δίνεται
από τη σχέση:
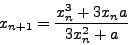 |
(38) |
Αν θέσω
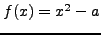 τότε
τότε 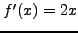 και
και 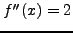 οπότε
αντικαθιστώντας στην αναδρομική σχέση Halleyκαταλήγω στη
ζητούμενη αναδρομική σχέση.
οπότε
αντικαθιστώντας στην αναδρομική σχέση Halleyκαταλήγω στη
ζητούμενη αναδρομική σχέση.
Ας χρησιμοποιήσουμε τις δύο σχέσεις για να υπολογίσουμε την ρίζα του
9. Αρα θα βρούμε τις ρίζες της εξίσωσης 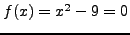 . Ας
θεωρήσουμε μιά αρχική τιμή
. Ας
θεωρήσουμε μιά αρχική τιμή 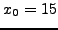 (αρκετά μακρυά από την
πραγματική ρίζα). Ο παρακάτω πίνακας μας δείχνει τα αποτελέσματα
από τις δύο μεθόδους.
(αρκετά μακρυά από την
πραγματική ρίζα). Ο παρακάτω πίνακας μας δείχνει τα αποτελέσματα
από τις δύο μεθόδους.
Table:
Σύγκριση των μεθόδων Newton-Raphsonκαι Halley
για την εύρεση της τετραγωνικής ρίζας του αριθμού 9.
| Newton-Raphson |
Σφάλμα |
Halley |
Σφαλμα |
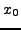 =15 =15 |
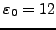 |
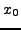 =15 =15 |
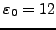 |
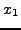 =7.8 =7.8 |
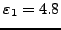 |
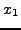 =5.526 =5.526 |
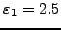 |
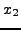 =4.477 =4.477 |
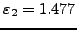 |
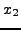 =3.16024 =3.16024 |
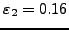 |
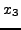 =3.2436 =3.2436 |
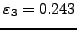 |
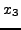 =3.00011 =3.00011 |
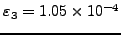 |
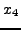 =3.0092 =3.0092 |
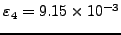 |
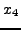 =3.0000000... =3.0000000... |
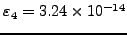 |
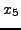 =3.00001 =3.00001 |
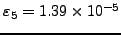 |
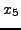 = 3.0000000... = 3.0000000... |
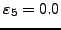 |
|
Figure:
Γραφική απεικόνιση του μη-γραμμικoύ συστήματoς
(1.39).
|
|





Next: ΣΥΣΤHΜAΤA ΜH-ΓΡAΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Up: Δεύτερης τάξης Newton-Raphson (Halley)
Previous: ΣΥΓΚΛΙΣΗ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() δίνεται
από τη σχέση:
δίνεται
από τη σχέση:
![]() . Ας
θεωρήσουμε μιά αρχική τιμή
. Ας
θεωρήσουμε μιά αρχική τιμή ![]() (αρκετά μακρυά από την
πραγματική ρίζα). Ο παρακάτω πίνακας μας δείχνει τα αποτελέσματα
από τις δύο μεθόδους.
(αρκετά μακρυά από την
πραγματική ρίζα). Ο παρακάτω πίνακας μας δείχνει τα αποτελέσματα
από τις δύο μεθόδους.