Estimate Of The Isoplanatic Angle Through the Scintilation Index

Almost all modern large telescopes are now being equipped with Adaptive Optics (AO) systems to compensate turbulence and to push the resolution to the diffraction limit at least at near-infrared wavelengths (Roddier, 1999). Good atmospheric seeing is even more critical to the AO operation than it is for classical seeing-limited observing. Moreover, atmospheric time constant 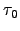$\tau_0$ and isoplanatic patch size 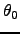$\theta_0$ are additional parameters which need to be known. Ideally, the vertical turbulence profile should also be monitored to assist AO operation. The time constant can be calculated with the theory presented in 2.1.2

The isoplanatic angle 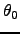$\theta_0$ can be estimated from the fluctuations of stellar flux received by the DIMM subapertures and caused by scintillations. It has been noted already by Loos & Hogge (1979) that the scintillation index in a 10-cm aperture can lead to an approximate estimation of 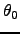$\theta_0$. Again, because of the too long exposure time of current DIMMs, the scintillation index is generally reduced by time averaging. However, this bias can be calculated providing that one has some real-time knowledge of the temporal spectrum of the scintillation.

Scintillation index 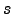$s$ is defined as a variance of the natural logarithm of the light intensity received by an aperture of the instrument. A theory of light propagation through atmosphere (Roddier, 1981) in the limit of faint perturbations relates the index to the vertical profile of the refractive index structure constant $C_n^2(h)$ :

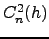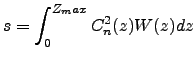$$s=\int_0^{Z_max}C_n^2(z)W(z)dz$$ (5.5)

where the integration over range 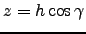$z=h\cos\gamma$ is performed from the aperture (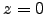$z=0$) to the maximum distance of turbulence, 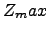$Z_max$. The weighting function 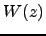$W(z)$ depends on turbulence spectrum, wavelength 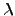$\lambda$, and aperture shape. For finite exposure time 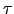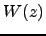$\tau$ , $W(z)$ is modified, because the "effective" aperture is extended in the wind direction by 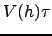$V(h)\tau$, where 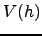$V(h)$ is the horizontal wind velocity at the altitude 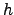$h$ above the obsevring site. 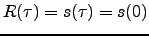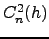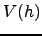Thus, a finite exposure time introduces the bias $R(\tau)=s(\tau)=s(0)$ in the measured scintillation index, which can be computed from the vertical profiles $C_n^2(h)$ and $V(h)$ (Tokovinin, 2001). The isoplanatic angle 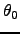$\theta_0$ at zenith (Fried, 1982) is defined as :

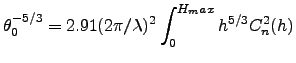$$\theta_0^{-5/3}=2.91(2\pi/\lambda)^2\int_0^{H_max}h^{5/3}C_n^2(h)$$ (5.6)

Loos & Hogge (1979) noted the similarity of equation 5.6 with equation 5.5, and suggested that 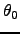$\theta_0$ can be derived from the scintillation index if the weighting function is roughly proportional to 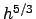$h^{5/3}$. For an aperture of about 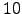$10$ cm in diameter and for 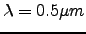$\lambda=0.5\mu m$ the approximation 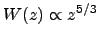$W(z) \propto z^{5/3}$ holds well at altitudes around 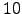$10$ km, which mostly contribute to scintillation. We calculate the isoplanatic angle (at zenith and at 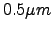$0.5\mu m$) from the scintillation index 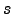$s$ measured at zenith angle 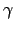$\gamma$ by the equation :

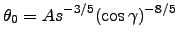$$\theta_0=As^{-3/5}(\cos\gamma)^{-8/5}$$ (5.7)

It is not clear, however, which value of the ratio 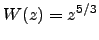$W(z)=z^{5/3}$ should be selected to compute the calibration constant 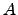$A$, and how this constant depends on 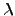$\lambda$ in an analytical manner. From various observations that M. Sarazin, & A. Tokovinin performed, calculated a value of 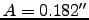$A=0.182''$ for a wavelength 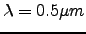$\lambda=0.5\mu m$ and this value is used here.