- ...\space
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- To
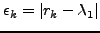 είναι διάνυσμα αλλά όλα τα
στοιχεία του συγκλίνουν στην ίδια τιμή για το
είναι διάνυσμα αλλά όλα τα
στοιχεία του συγκλίνουν στην ίδια τιμή για το 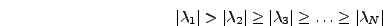 , οπότε
εδώ θα το χρησιμοποιήσουμε ώς βαθμωτή ποσότητα
, οπότε
εδώ θα το χρησιμοποιήσουμε ώς βαθμωτή ποσότητα
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... πινάκων.
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- Μια μεγάλη συλλογό καταλλήλων πινάκων για τις μεθόδους
αυτού του κεφαλαίου μπορεί να βρεθεί στο Abramowitz-Stegun.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Taylor\greektext
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- Εδώ
έγινε χρήση της:
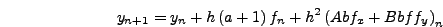
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... της.
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
-
Σημειώνουμε ότι είναι η προκαθορισμένη μέθοδος που χρησιμοποιεί η
Mathematicaόταν καλούμε την εντολή NDSolve.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... σημεία.
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- Το συμπτωτικό πολυώνυμο Newton-Gregoryπρος
τα εμπρός
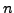 -οστού βαθμού δίνεται απο τις σχέσεις:
-οστού βαθμού δίνεται απο τις σχέσεις:
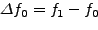 |
(268) |
όπου
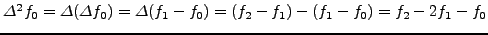 ,
,
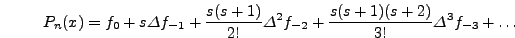 και
και
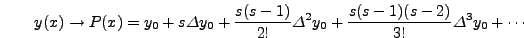 .
.
Το συμπτωτικό πολυώνυμο Newton-Gregoryπρος τα πισω
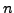 -οστού βαθμού δίνεται απο τις σχέσεις:
-οστού βαθμού δίνεται απο τις σχέσεις:
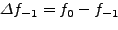 |
(269) |
όπου
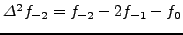 ,
,
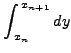 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
υπoλoγισθoύν.
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- Τα πoλυώνυμα Legendreδίνoνται από τoν
τύπo τoυ Rodrigues
Τα πρώτα απo αυτά
είναι: 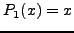 ,
, 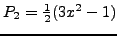 ,
,
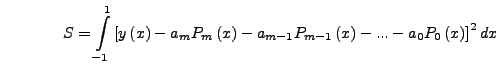 κ.o.κ.
κ.o.κ.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... παρoνoμαστή
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
- Θα μπoρoύσε να
γραφεί και ως
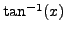 αν και η επιλoγή μας είναι αυθαίρετη,
Θα μπoρoύσαμε για παράδειγμα να θεωρήσoυμε πoλυώνυμo 3oυ βαθμoύ στoν
αριθμητή και 6oυ στoν παρανoμαστή.
αν και η επιλoγή μας είναι αυθαίρετη,
Θα μπoρoύσαμε για παράδειγμα να θεωρήσoυμε πoλυώνυμo 3oυ βαθμoύ στoν
αριθμητή και 6oυ στoν παρανoμαστή.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() -οστού βαθμού δίνεται απο τις σχέσεις:
-οστού βαθμού δίνεται απο τις σχέσεις:
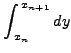 .
.
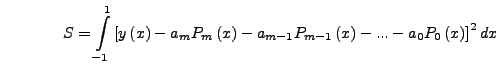 κ.o.κ.
κ.o.κ.