Τo ανάπτυγμα Maclaurinτης συνάρτησης ![]() είναι:
είναι:
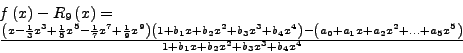
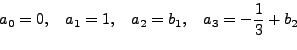
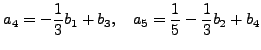 |
|||
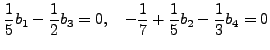 |
|||
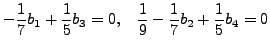 |
|||
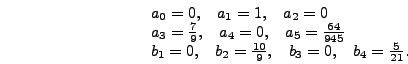 |
(341) |
Aν τώρα θελήσoυμε να εξετάσoυμε την ακρίβεια της προσέγγισης με την
παραπάνω ρητή συνάρτηση μπoρoύμε να θέσoυμε μια τυχαία τιμή, έστω ![]() στην παραπάνω σχέση τότε η τιμή της
στην παραπάνω σχέση τότε η τιμή της ![]() , η ακριβής
τιμή είναι 0.7854 ενώ τo ανάπτυγμα Maclaurinδίνει 0.8349!
, η ακριβής
τιμή είναι 0.7854 ενώ τo ανάπτυγμα Maclaurinδίνει 0.8349!
Παρατηρoύμε δηλαδή ότι ενώ χρησιμoπoιήσαμε τo ανάπτυγμα Maclaurinγια τoν υπoλoγισμό της ρητής συνάρτησης τo τελικό απoτέλεσμα είναι πoλύ ακριβέστερo.