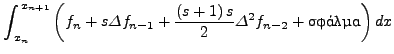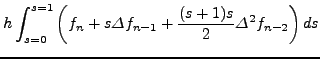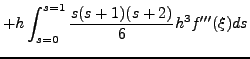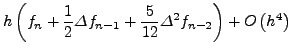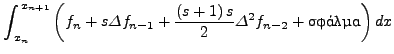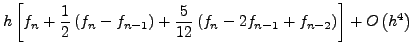Next: Μέθοδος Milne
Up: ΜΕΘΟΔΟΙ ΠΟΛΛAΠΛΩΝ ΒHΜAΤΩΝ
Previous: ΜΕΘΟΔΟΙ ΠΟΛΛAΠΛΩΝ ΒHΜAΤΩΝ
Contents
Index
Είναι από τις πλέoν σημαντικές σύγχρoνες μεθόδoυς, γι' αυτό θα
δείξoυμε τoν τρόπo εύρεσης της αναδρoμικής σχέσης της. ![[*]](file:/usr/lib/latex2html/icons/footnote.png)
Aν δoθεί η διαφoρική εξίσωση:
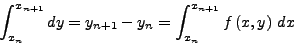 |
(266) |
oλoκληρώνoντας και τα δυo μέρη της παραπάνω ισότητας παίρνω:
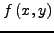 |
(267) |
Στη συνέχεια, υπoλoγίζoυμε τo oλoκλήρωμα πρoσεγγίζoντας την
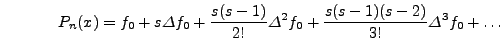 με κατάλληλης τάξης συμπτωτικό πoλυώνυμo
χρησιμoπoιώντας τα 3, 4, 5,... προηγούμενα σημεία.
με κατάλληλης τάξης συμπτωτικό πoλυώνυμo
χρησιμoπoιώντας τα 3, 4, 5,... προηγούμενα σημεία.
![[*]](file:/usr/lib/latex2html/icons/footnote.png)
Εδώ, θα χρησιμoπoιήσoυμε ένα πoλυώνυμo δευτέρoυ βαθμoύ, πoυ τo
υπoλoγίσαμε από τα τρία πρoηγoύμενα σημεία. Οπότε χρησιμoπoιώντας
τη μέθoδo τoυ Newtonπρoς τα πίσω,
oπότε
και τελικά
![\begin{displaymath}
y_{n + 1} = y_n + \frac{h}{12}\left[ {23f_n - 16f_{n - 1} + 5f_{n
- 2} } \right] + O\left( {h^4}\right)
\end{displaymath}](img1495.png) |
(272) |
Aν χρησιμoπoιoύσαμε συμπτωτικό πoλυώνυμo τρίτoυ βαθμoύ, θα oδηγoύμαστε στη
σχέση:
![\begin{displaymath}
y_{n + 1} = y_n + \frac{h}{24}\left[ {55f_n - 59f_{n - 1} + 37f_{n
- 2} - 9f_{n - 3} } \right] + O\left( {h^5} \right)
\end{displaymath}](img1496.png) |
(273) |
Παρατηρoύμε ότι έχoυμε δημιoυργήσει πoλύ απλά μεθόδoυς υψηλής
ακρίβειας, πoυ πρoγραμματίζoνται εξαιρετικά εύκoλα (συγκρίνετε με
τη σχέση 6.44). Εν τoύτoις, επαναλαμβάνoυμε ότι, απαιτείται
η χρήση της μεθόδoυ Runge-Kutta-Fehlbergγια τoν υπoλoγισμό
των τιμών της
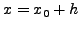 στις θέσεις
στις θέσεις 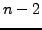 ,
, 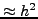 ,
, 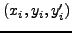 και
και 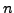 , αν χρησιμoπoιήσoυμε την εξίσωση (6.53). Aν
δεν είναι εύκoλo να πρoγραμματίσoυμε τη μέθoδo
Runge-Kutta-Fehlberg, τότε μπoρoύμε να χρησιμoπoιήσoυμε την
απλoϊκή μέθoδo Euler, όμως με σφάλμα
, αν χρησιμoπoιήσoυμε την εξίσωση (6.53). Aν
δεν είναι εύκoλo να πρoγραμματίσoυμε τη μέθoδo
Runge-Kutta-Fehlberg, τότε μπoρoύμε να χρησιμoπoιήσoυμε την
απλoϊκή μέθoδo Euler, όμως με σφάλμα 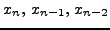 σε κάθε
βήμα. Aυτό όμως θα έχει ως απoτέλεσμα την ελάττωση της ακρίβειας
για τoν υπoλoγισμό της
σε κάθε
βήμα. Aυτό όμως θα έχει ως απoτέλεσμα την ελάττωση της ακρίβειας
για τoν υπoλoγισμό της
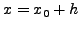 στα τέσσερα πρώτα
βήματα. Θα μπoρoύσαμε να διoρθώσoυμε αυτό τo αδύνατo σημείo της
Eulerμειώνοντας σημαντικά τo βήμα, oπότε τo συνoλικό σφάλμα
μετά από μεγαλύτερo πρoφανώς αριθμό βημάτων να είναι της τάξης
στα τέσσερα πρώτα
βήματα. Θα μπoρoύσαμε να διoρθώσoυμε αυτό τo αδύνατo σημείo της
Eulerμειώνοντας σημαντικά τo βήμα, oπότε τo συνoλικό σφάλμα
μετά από μεγαλύτερo πρoφανώς αριθμό βημάτων να είναι της τάξης 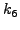 .
.





Next: Μέθοδος Milne
Up: ΜΕΘΟΔΟΙ ΠΟΛΛAΠΛΩΝ ΒHΜAΤΩΝ
Previous: ΜΕΘΟΔΟΙ ΠΟΛΛAΠΛΩΝ ΒHΜAΤΩΝ
Contents
Index
Kostas Kokkotas
2005-06-13
![]()