




Next: ΑΝΑΔΡΟΜΙΚΗ ΣΧΕΣΗ
Up: ΡΙΖΕΣ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Previous: ΣΥΓΚΛΙΣΗ
Contents
Index
Η ΜΕΘΟΔΟΣ ΤΟΥ MULLER
Η μέθοδος Mullerαποτελεί επέκταση της μεθόδου της γραμμικής
παρεμβολής και αντί να προσεγγίζει την συνάρτηση με ευθεία την
προσέγγιζει με παραβολή.
Αν δοθούν τρεις αρχικές τιμές
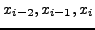 ,
υποθέτουμε ότι η
,
υποθέτουμε ότι η 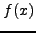 προσεγγίζεται από ένα 2ο-βάθμιο πολυώνυμο
προσεγγίζεται από ένα 2ο-βάθμιο πολυώνυμο
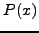 του οποίου εύκολα υπολογίζουμε τις ρίζες. Για τις τρεις
αρχικές τιμές του
του οποίου εύκολα υπολογίζουμε τις ρίζες. Για τις τρεις
αρχικές τιμές του 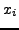 λαμβάνουμε τρείς εξισώσεις της μορφής :
λαμβάνουμε τρείς εξισώσεις της μορφής :
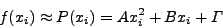 |
(20) |
από τις οποίες υπολογίζουμε τους 3 συντελεστές του τριωνύμου μέσω
των σχέσεων
όπου
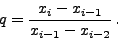 |
(22) |
Οπότε η επόμενη προσεγγιστική τιμή 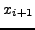 βρίσκεται
ως η ρίζα της παραβολής
βρίσκεται
ως η ρίζα της παραβολής
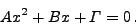 |
(23) |
Subsections
Kostas Kokkotas
2005-06-13
![]() ,
υποθέτουμε ότι η
,
υποθέτουμε ότι η ![]() προσεγγίζεται από ένα 2ο-βάθμιο πολυώνυμο
προσεγγίζεται από ένα 2ο-βάθμιο πολυώνυμο
![]() του οποίου εύκολα υπολογίζουμε τις ρίζες. Για τις τρεις
αρχικές τιμές του
του οποίου εύκολα υπολογίζουμε τις ρίζες. Για τις τρεις
αρχικές τιμές του ![]() λαμβάνουμε τρείς εξισώσεις της μορφής :
λαμβάνουμε τρείς εξισώσεις της μορφής :