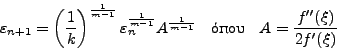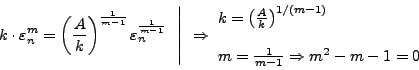Next: Η ΜΕΘΟΔΟΣ ΤΟΥ MULLER
Up: Η ΜΕΘΟΔΟΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ
Previous: ΚΡΙΤΙΚΗ
Contents
Index
ΣΥΓΚΛΙΣΗ
Έστω 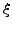 η ακριβής ρίζα της
εξίσωσης. Αν θεωρήσουμε ότι
η ακριβής ρίζα της
εξίσωσης. Αν θεωρήσουμε ότι
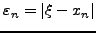 είναι το σφάλμα στην εύρεση της ρίζας της
είναι το σφάλμα στην εύρεση της ρίζας της
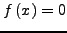 για
για 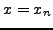 , τότε η μέθοδος της γραμμικής παρεμβολής συγκλίνει με βάση
τη σχέση
, τότε η μέθοδος της γραμμικής παρεμβολής συγκλίνει με βάση
τη σχέση
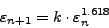 |
(14) |
Η απόδειξη αυτής της σχέσης, μπορεί να χρησιμοποιηθεί και ώς βάση
γαι τον υπολογισμό της ταχύτητας σύγκλισης και άλλων μεθόδων αυτού
του κεφαλαίου.
Εστω η αναδρομική σχέση
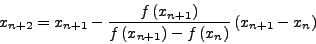 |
(15) |
τότε
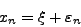 |
(16) |
όπου
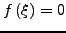 . Δηλαδή,
. Δηλαδή,
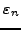 είναι η
« απόσταση » (το σφάλμα) της
είναι η
« απόσταση » (το σφάλμα) της 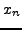 από την ακριβή ρίζα της
εξίσωσης
από την ακριβή ρίζα της
εξίσωσης 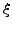 . Επομένως αν θεωρήσουμε ένα ανάπτυγμα Taylor
για κάθε μιά από τις τρείς τιμές
. Επομένως αν θεωρήσουμε ένα ανάπτυγμα Taylor
για κάθε μιά από τις τρείς τιμές 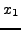 ,
, 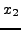 και
και 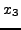
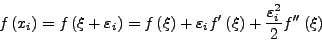 |
(17) |
και αντικαταστήσουμε τα αναπτύγματα στην αρχική σχέση βρίσκουμε
η σχέση αυτή μετά από μερικές απλοποιήσεις οδηγεί στην:
η οποία συνδέει το σφάλμα στο βήμα 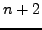 με τα σφάλματα
στα βήματα
με τα σφάλματα
στα βήματα 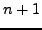 και
και 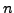 .
.
Το ζητούμενο όμως είναι μια σχέση της μορφής
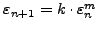 όπου τα
όπου τα 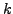 και
και 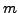 ειναι
άγνωστες σταθερές. Για τον υπολογισμό μιας σχέσης αυτής της μορφής
θα εργασθούμε ως εξης: τα σφάλματα στις επαναλήψεις
ειναι
άγνωστες σταθερές. Για τον υπολογισμό μιας σχέσης αυτής της μορφής
θα εργασθούμε ως εξης: τα σφάλματα στις επαναλήψεις 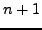 και
και
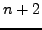 είναι
είναι
και τελικά λαμβάνουμε
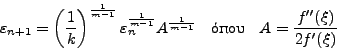 |
(18) |
οπότε αντικαθιστώντας και το
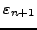 οδηγούμε σε μια σχέση μόνο για το
οδηγούμε σε μια σχέση μόνο για το
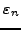 από την οποία
θα προσπαθήσουμε να υπολογίσουμε τις τιμές του
από την οποία
θα προσπαθήσουμε να υπολογίσουμε τις τιμές του 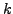 και
και 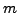 . Άρα
. Άρα
Άρα
Οποτε τελικά καταλήγουμε στη ζητούμενη σχέση:
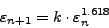 |
(19) |
Παρατηρούμε ότι η σύγκλιση της μεθόδου δεν είναι γραμμική
αλλά περιπού τετραγωνική και προφανώς η εύρεση της ρίζας μιας
εξίσωσης απαιτεί σημαντικά μικρότερο αριθμό αριθμητικών πράξεων.





Next: Η ΜΕΘΟΔΟΣ ΤΟΥ MULLER
Up: Η ΜΕΘΟΔΟΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ
Previous: ΚΡΙΤΙΚΗ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() η ακριβής ρίζα της
εξίσωσης. Αν θεωρήσουμε ότι
η ακριβής ρίζα της
εξίσωσης. Αν θεωρήσουμε ότι
![]() είναι το σφάλμα στην εύρεση της ρίζας της
είναι το σφάλμα στην εύρεση της ρίζας της
![]() για
για ![]() , τότε η μέθοδος της γραμμικής παρεμβολής συγκλίνει με βάση
τη σχέση
, τότε η μέθοδος της γραμμικής παρεμβολής συγκλίνει με βάση
τη σχέση
![]() όπου τα
όπου τα ![]() και
και ![]() ειναι
άγνωστες σταθερές. Για τον υπολογισμό μιας σχέσης αυτής της μορφής
θα εργασθούμε ως εξης: τα σφάλματα στις επαναλήψεις
ειναι
άγνωστες σταθερές. Για τον υπολογισμό μιας σχέσης αυτής της μορφής
θα εργασθούμε ως εξης: τα σφάλματα στις επαναλήψεις ![]() και
και
![]() είναι
είναι