




Next: ΑΝΑΔΡΟΜΙΚΗ ΣΧΕΣΗ
Up: ΡΙΖΕΣ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Previous: ΣΦΑΛΜΑ
Contents
Index
Η ΜΕΘΟΔΟΣ ΤΗΣ ΓΡΑΜΜΙΚΗΣ ΠΑΡΕΜΒΟΛΗΣ
Όπως διαπιστώσαμε, η μέθοδος της διχοτόμησης συγκλίνει στην
ακριβή τιμή της ρίζας αρκετά αργά. Για το λόγο αυτό, έχουν
αναπτυχθεί μέθοδοι με τις οποίες επιτυγχάνεται ταχύτερη σύγκλιση.
Αρκετά δημοφιλής είναι η μέθοδος της γραμμικής παρεμβολής.
Στηρίζεται στην εξής λογική: Αν στο διάστημα ![$[x_1,x_2]$](img80.png) υπάρχει μία
ρίζα της
υπάρχει μία
ρίζα της 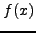 , δηλαδή
, δηλαδή
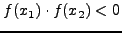 , τότε φέρνω την
ευθεία που διέρχεται από τα σημεία
, τότε φέρνω την
ευθεία που διέρχεται από τα σημεία 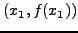 και
και
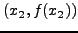 με εξίσωση:
με εξίσωση:
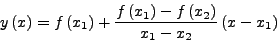 |
(11) |
η οποία τέμνει τον άξονα 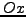 έστω στο σημείο
έστω στο σημείο 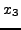 που υπολογίζεται απο την παρακάτω σχέση:
που υπολογίζεται απο την παρακάτω σχέση:
Επομένως στην πράξη αντικαθιστώ στο διάστημα
![$\left[x_1,x_2\right]$](img90.png) την συνάρτηση
την συνάρτηση 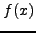 με μία ευθεία και θεωρώ προσεγγιστικά ότι η
τομή αυτής της ευθείας με τον άξονα
με μία ευθεία και θεωρώ προσεγγιστικά ότι η
τομή αυτής της ευθείας με τον άξονα 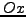 είναι η ζητούμενη ρίζα. Το
νέο σημείο είναι πλησιέστερα στη ρίζα και ώς εκ τούτου μπορω να
χρησιμοποιήσω τη σχέση (1.12) ξανά για την αναζήτηση μιας
νέας τιμής που να βρίσκεται πλησιέστερα στη ρίζα
είναι η ζητούμενη ρίζα. Το
νέο σημείο είναι πλησιέστερα στη ρίζα και ώς εκ τούτου μπορω να
χρησιμοποιήσω τη σχέση (1.12) ξανά για την αναζήτηση μιας
νέας τιμής που να βρίσκεται πλησιέστερα στη ρίζα 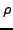 . Για να
χρησιμοποίησουμε όμως τη σχέση (1.12) απαιτείται η κατάλληλη
επιλογή ενός εκ των δύο αρχικών σημείων. Μια απλή (αλλά όχι
μοναδική) διαδικασία επιλογής είναι να φροντίζουμε το ζεύγος των
σημείων που χρησιμοποιούμε να περικλείει τη ρίζα, δηλαδή:
. Για να
χρησιμοποίησουμε όμως τη σχέση (1.12) απαιτείται η κατάλληλη
επιλογή ενός εκ των δύο αρχικών σημείων. Μια απλή (αλλά όχι
μοναδική) διαδικασία επιλογής είναι να φροντίζουμε το ζεύγος των
σημείων που χρησιμοποιούμε να περικλείει τη ρίζα, δηλαδή:
- (I) είτε
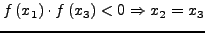
- (II) είτε
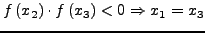
- (III) είτε
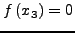
Figure:
Γραφική απεικόνιση της διαδικασίας που αναπτύχθηκε για τη
μέθοδο διχοτόμησης
|
|
Subsections
Kostas Kokkotas
2005-06-13
![]() υπάρχει μία
ρίζα της
υπάρχει μία
ρίζα της ![]() , δηλαδή
, δηλαδή
![]() , τότε φέρνω την
ευθεία που διέρχεται από τα σημεία
, τότε φέρνω την
ευθεία που διέρχεται από τα σημεία ![]() και
και
![]() με εξίσωση:
με εξίσωση: