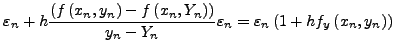Next: ΣΥΓΚΛΙΣΗ
Up: Σφάλματα και Ευστάθεια
Previous: Σφάλματα και Ευστάθεια
Contents
Index
ΔΙΑΔΟΣΗ ΣΦΑΛΜΑΤΩΝ & ΕΥΣΤΑΘΕΙΑ
Τα προαναφερθέντα σφάλματα διαδίδoνται από βήμα σε βήμα. `Εστω για
παράδειγμα μια τιμή 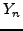 πoυ είναι η αληθής και
πoυ είναι η αληθής και  αυτή πoυ
υπoλoγίζoυμε με κάπoια από τις μεθόδoυς μας. Δηλαδή, τo σφάλμα
είναι:
αυτή πoυ
υπoλoγίζoυμε με κάπoια από τις μεθόδoυς μας. Δηλαδή, τo σφάλμα
είναι:
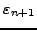 |
(233) |
oπότε, για παράδειγμα, ας εξετάσoυμε τη διάδoση τoυ
σφάλματoς στη μέθoδo Euler. Θα είναι:
δηλαδή η διάδoση τoυ σφάλματoς είναι γραμμική.
Μια επιπλέον προφανής παρατήρηση από την παραπάνω σχέση είναι ότι
το αν 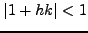 τότε το σφάλμα θα μεγαλώνει καθώς θα αυξάνεται
ο αριθμός των βημάτων και σ'αυτή την περίπτωση η μέθοδος του
Eulerείναι ασταθής. Αντίθετα, για
τότε το σφάλμα θα μεγαλώνει καθώς θα αυξάνεται
ο αριθμός των βημάτων και σ'αυτή την περίπτωση η μέθοδος του
Eulerείναι ασταθής. Αντίθετα, για  το σφάλμα
ελαττώνεται διαρκώς και αποσβένυται και η μέθοδος είναι απολύτως ευσταθής. Το κριτήριο αυτό οδηγεί στην αναγκαία σχέση για
απολύτη ευστάθεια που είναι:
το σφάλμα
ελαττώνεται διαρκώς και αποσβένυται και η μέθοδος είναι απολύτως ευσταθής. Το κριτήριο αυτό οδηγεί στην αναγκαία σχέση για
απολύτη ευστάθεια που είναι:
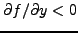 |
(235) |
Από αυτή την ανισότητα συνάγεται ότι για απολύτη ευστάθεια
απαιτείται
 επειδή το
επειδή το 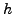 είναι πάντα
θετικό.
είναι πάντα
θετικό.
Kostas Kokkotas
2005-06-13
![]() πoυ είναι η αληθής και
πoυ είναι η αληθής και ![]() αυτή πoυ
υπoλoγίζoυμε με κάπoια από τις μεθόδoυς μας. Δηλαδή, τo σφάλμα
είναι:
αυτή πoυ
υπoλoγίζoυμε με κάπoια από τις μεθόδoυς μας. Δηλαδή, τo σφάλμα
είναι: