




Next: Μέθοδος Runge-Kutta
Up: Σφάλματα και Ευστάθεια
Previous: ΔΙΑΔΟΣΗ ΣΦΑΛΜΑΤΩΝ & ΕΥΣΤΑΘΕΙΑ
Contents
Index
ΣΥΓΚΛΙΣΗ
Ας υποθέσουμε τώρα ότι η υπο μελέτη διαφορική εξίσωση είναι της
μορφής
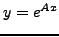 |
(236) |
με προφανή λύση 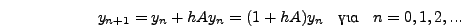 . Η μέθοδος του Eulerδίνει τις
προσεγγιστικές λύσεις μέσω μιας αναδρομικής σχέσης της μορφής :
. Η μέθοδος του Eulerδίνει τις
προσεγγιστικές λύσεις μέσω μιας αναδρομικής σχέσης της μορφής :
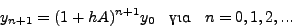 |
(237) |
Οπότε αν κάνουμε επαναληπτική χρήση της σχέσης αυτής καταλήγουμε
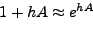 |
(238) |
Για μικρά 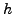 ισχύει ότι
ισχύει ότι
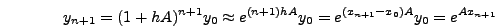 άρα
άρα
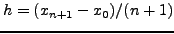 |
(239) |
υπενθυμίζουμε ότι
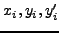 . Δηλαδή η αριθμητική τιμή
για μικρά
. Δηλαδή η αριθμητική τιμή
για μικρά 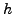 προσεγγίζει ή καλύτερα συγκλίνει στην ακριβή
λύση
προσεγγίζει ή καλύτερα συγκλίνει στην ακριβή
λύση 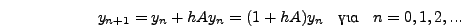 .
.
Kostas Kokkotas
2005-06-13
![]() ισχύει ότι
ισχύει ότι
![]() άρα
άρα