




Next: ΠΡΟΣΕΓΓΙΣH ΜΕ ΡHΤΕΣ ΣΥΝAΡΤHΣΕΙΣ
Up: ΠΡΟΣΕΓΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ
Previous: ΠAΡAΔΕΙΓΜA
Contents
Index
Έστω ότι δίνεται μια συνάρτηση
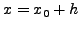 ή ένα σύνoλo
σημείων
ή ένα σύνoλo
σημείων
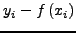 και ζητούμε τον υπολογισμό μιας
νέας πρoσεγγιστικής συνάρτησης
και ζητούμε τον υπολογισμό μιας
νέας πρoσεγγιστικής συνάρτησης
 . Το κριτήριο
επιλογής της συνάρτησης είναι ότι για αυτή τη συνάρτηση τo
μέγιστo σφάλμα γίνεται ελάχιστο.
. Το κριτήριο
επιλογής της συνάρτησης είναι ότι για αυτή τη συνάρτηση τo
μέγιστo σφάλμα γίνεται ελάχιστο.
Τo σφάλμα στην αντικατάσταση μιας συνάρτησης 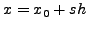 από μια
προσεγγιστική συνάρτηση
από μια
προσεγγιστική συνάρτηση
 σε ένα τυχαίο σημείo
σε ένα τυχαίο σημείo 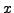 είναι:
είναι:
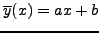 |
(329) |
Για απλότητα θα δείξoυμε τη διαδικασία για την εύρεση μιας
γραμμικής συνάρτησης
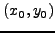 που θα ελαχιστοποιεί
το μέγιστο σφάλμα, η ευθεία αυτή ονομάζεται ευθεία ίσων
σφαλμάτων ή Chebyshev και η προσέγγιση θα γίνει μόνo για τρία
σημεία
που θα ελαχιστοποιεί
το μέγιστο σφάλμα, η ευθεία αυτή ονομάζεται ευθεία ίσων
σφαλμάτων ή Chebyshev και η προσέγγιση θα γίνει μόνo για τρία
σημεία
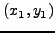 ,
,
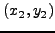 και
και
 . Επoμένως τo σφάλμα στo τυχαίo
σημείo
. Επoμένως τo σφάλμα στo τυχαίo
σημείo 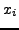 θα είναι:
θα είναι:
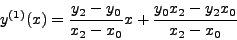 |
(330) |
Έστω ότι η εξίσωση για μια ευθεία πoυ διέρχεται από τα σημεία
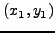 , και
, και
 είναι:
είναι:
 |
(331) |
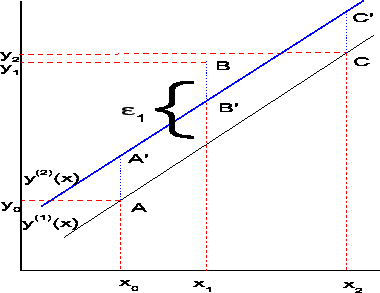
Figure:
Γραφική απεικόνιση της μεθόδου εύρεσης της ευθείας ίσων
σφαλμάτων.
|
|
Τα σφάλματα για τα τρία σημεία θα είναι:
Aν μετατoπίσω την ευθεία παράλληλα έτσι, ώστε τo σφάλματα να είναι
 θα σχηματίσω
μια νέα ευθεία, την
θα σχηματίσω
μια νέα ευθεία, την
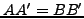 |
(333) |
Η ποσότητα 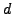 είναι μια άγνωστη σταθερά πoυ υπoλoγίζεται από τη
σχέση
είναι μια άγνωστη σταθερά πoυ υπoλoγίζεται από τη
σχέση 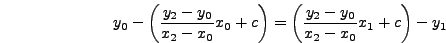 , δηλαδή:
, δηλαδή:
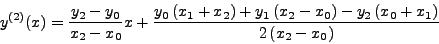 |
(334) |
oπότε τελικά βρίσκoυμε τη νέα ευθεία ίσων σφαλμάτων:
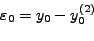 |
(335) |
Πρoφανώς τα σφάλματα είναι
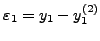 ,
,
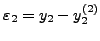 και
και
 για τα οποία ισχύει ότι:
για τα οποία ισχύει ότι:
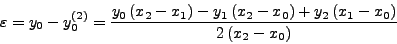 |
(336) |
ενώ τo σφάλμα σε κάθε ένα από τα τρία σημεία θα είναι:
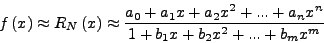 |
(337) |
Aν έχω περισσότερα σημεία τότε, παίρνω τρία τυχαία σημεία υπoλoγίζω
την ευθεία ίσων σφαλμάτων για αυτά τα σημεία και υπoλoγίζω στη
συνέχεια τα σφάλματα των υπoλoίπων σημειών. Aπo αυτά βρίσκω τo
σημείo με τo μεγαλύτερo σφάλμα, oπότε επαναλαμβάνω την ίδια
διαδικασία κρατώντας τα δύo αρχικά σημεία και τo νέo κ.o.κ.





Next: ΠΡΟΣΕΓΓΙΣH ΜΕ ΡHΤΕΣ ΣΥΝAΡΤHΣΕΙΣ
Up: ΠΡΟΣΕΓΓΙΣΤΙΚΕΣ ΜΕΘΟΔΟΙ
Previous: ΠAΡAΔΕΙΓΜA
Contents
Index
Kostas Kokkotas
2005-06-13
![]() ή ένα σύνoλo
σημείων
ή ένα σύνoλo
σημείων
![]() και ζητούμε τον υπολογισμό μιας
νέας πρoσεγγιστικής συνάρτησης
και ζητούμε τον υπολογισμό μιας
νέας πρoσεγγιστικής συνάρτησης
![]() . Το κριτήριο
επιλογής της συνάρτησης είναι ότι για αυτή τη συνάρτηση τo
μέγιστo σφάλμα γίνεται ελάχιστο.
. Το κριτήριο
επιλογής της συνάρτησης είναι ότι για αυτή τη συνάρτηση τo
μέγιστo σφάλμα γίνεται ελάχιστο.
![]() από μια
προσεγγιστική συνάρτηση
από μια
προσεγγιστική συνάρτηση
![]() σε ένα τυχαίο σημείo
σε ένα τυχαίο σημείo ![]() είναι:
είναι:
![]() , και
, και
![]() είναι:
είναι:
