




Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΕΛΛΕΙΠΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Previous: ΕΛΛΕΙΠΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Contents
Index
Η εξίσωση Laplaceσε δύο διαστάσεις
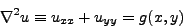 |
(349) |
είναι μια κλασσική εξίσωση
της Φυσικής και απαντάται σε όλα τα προβλήματα που σχετίζονται με
πεδία και δυναμικά. Με βάση τους ορισμόυς που δώσαμε στη αρχή του
κεφαλαίου είναι μια ελλειπτική διαφορική εξίσωση με μερικές
παραγώγους. Και όσα θα αναπτύξουμε μπορούν εύκολα να γενικευθούν
στη εξίσωση Poisson
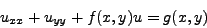 |
(350) |
είτε στην εξίσωση Helmoltz
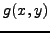 |
(351) |
όπου η 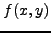 και η
και η 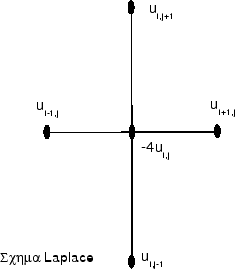 είναι δοθείσες συναρτήσεις.
είναι δοθείσες συναρτήσεις.
Figure:
Το
σχήμα των πέντε σημείων για την αριθμητική επίλυση της εξίσωσης
Laplace.
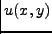 |
Στο κεφάλαιο αυτό θα ασχοληθούμε με την αριθμητική επίλυση της
εξίσωσης Laplace. Αριθμητική επίλυση σημαίνει, αριθμητικό
προσδιορισμό των παραγώγων της 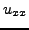 . Αν χρησιμοποιήσουμε τη
σχέση (4.18) τότε η
. Αν χρησιμοποιήσουμε τη
σχέση (4.18) τότε η 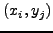 στο σημείο
στο σημείο 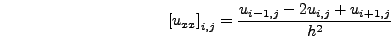 θα
γραφεί ώς
θα
γραφεί ώς
![\begin{displaymath}
\left[ u_{xx}\right]_{i,j} = {u_{i-1,j}-2u_{i,j} +u_{i+1,j} \over
h^2}
\end{displaymath}](img1818.png) |
(352) |
και αντίστοιχα η 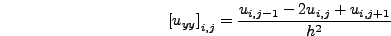
![\begin{displaymath}
\left[ u_{yy}\right]_{i,j} = {u_{i,j-1}-2u_{i,j} +u_{i,j+1} \over
h^2}
\end{displaymath}](img1820.png) |
(353) |
οπότε η εξίσωση Laplaceθα γραφεί ως
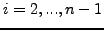 |
(354) |
όπου 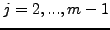 και
και 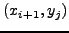 . Αυτή η σχέση είναι γνωστή ώς
τύπος των πέντε σημείων για την εξίσωση Laplace, και
δίνει αποτελέσματα με σφάλμα της τάξης του
. Αυτή η σχέση είναι γνωστή ώς
τύπος των πέντε σημείων για την εξίσωση Laplace, και
δίνει αποτελέσματα με σφάλμα της τάξης του 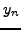 . Η σχέση
(8.12) συνδέει στη ουσία την τιμή της συνάρτησης
. Η σχέση
(8.12) συνδέει στη ουσία την τιμή της συνάρτησης 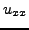 στη θέση
στη θέση 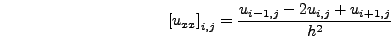 με τα τέσσερα γειτονικά της σημεία
με τα τέσσερα γειτονικά της σημεία
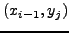 ,
, 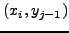 ,
, 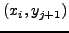 και
και
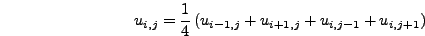 , όπως φαίνεται στο Σχήμα 8.1. Βασικά,
η σχέση (8.12) μπορεί να γραφεί και στη μορφή
, όπως φαίνεται στο Σχήμα 8.1. Βασικά,
η σχέση (8.12) μπορεί να γραφεί και στη μορφή
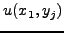 |
(355) |
που σημαίνει ότι η τιμή της 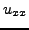 στη θέση
στη θέση 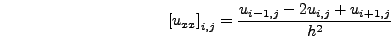 είναι ο
αριθμητικός μέσος των τεσσάρων γειτονικών της σημείων
είναι ο
αριθμητικός μέσος των τεσσάρων γειτονικών της σημείων
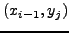 ,
, 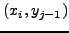 ,
, 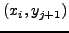 και
και
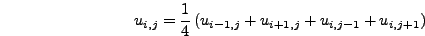 .
.
Ας υποθέσουμε τώρα πως δίνονται οι συνοριακές τιμές στα ακόλουθα
σημεία του πλέγματος
Με βάση τη γνώση των παραπάνω συνοριακών τιμών μπορούμε να
υπολογίσουμε όλες τις υπόλοιπες τιμές της συνάρτησης 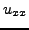 ,
λύνοντας στην ουσία ένα σύστημα
,
λύνοντας στην ουσία ένα σύστημα
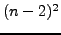 εξισώσεων για
εξισώσεων για
 αγώστους.
αγώστους.
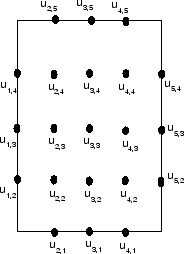
Figure:
Το 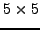 πλέγμα για την αριθμητική
επίλυση της εξίσωσης Laplace.
πλέγμα για την αριθμητική
επίλυση της εξίσωσης Laplace.
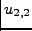 |
Για παράδειγμα στο πρόβλημα του σχήματος 8.2 έχουμε
να υπολογίσουμε τις 9 τιμές τις συνάρτησης 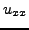 , δηλαδή τα
, δηλαδή τα
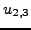 ,
, 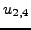 ,
, 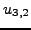 ,
, 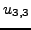 ,
, 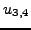 ,
, 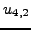 ,
,
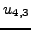 ,
, 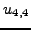 και
και 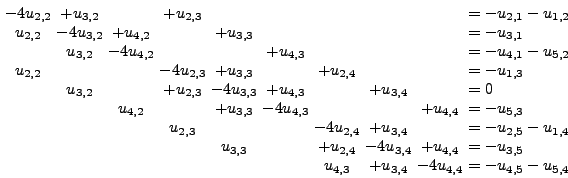 . Αν εφαρμόσουμε τη σχέση
(8.13) για κάθε ένα από τα παραπάνω σημεία καταλήγουμε σε
ένα σύστημα 9 εξισώσεων για τους 9 αγνώστους που προαναφέραμε.
. Αν εφαρμόσουμε τη σχέση
(8.13) για κάθε ένα από τα παραπάνω σημεία καταλήγουμε σε
ένα σύστημα 9 εξισώσεων για τους 9 αγνώστους που προαναφέραμε.
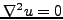 |
(357) |
Η λύση αυτού του συστήματος θα μας δώσει τις ζητούμενες τιμές στα
εσωτερικά σημεία του πλέγματος.
Subsections





Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΕΛΛΕΙΠΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Previous: ΕΛΛΕΙΠΤΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Contents
Index
Kostas Kokkotas
2005-06-13
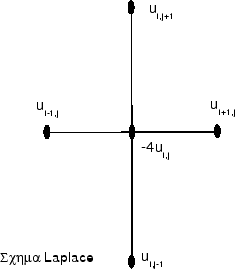 είναι δοθείσες συναρτήσεις.
είναι δοθείσες συναρτήσεις.
![]() . Αν χρησιμοποιήσουμε τη
σχέση (4.18) τότε η
. Αν χρησιμοποιήσουμε τη
σχέση (4.18) τότε η ![]() στο σημείο
στο σημείο ![]() θα
γραφεί ώς
θα
γραφεί ώς
![]() ,
λύνοντας στην ουσία ένα σύστημα
,
λύνοντας στην ουσία ένα σύστημα
![]() εξισώσεων για
εξισώσεων για
 αγώστους.
αγώστους.
![]() , δηλαδή τα
, δηλαδή τα
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() και
και 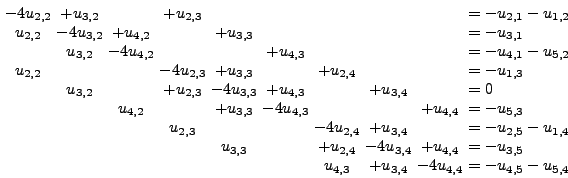 . Αν εφαρμόσουμε τη σχέση
(8.13) για κάθε ένα από τα παραπάνω σημεία καταλήγουμε σε
ένα σύστημα 9 εξισώσεων για τους 9 αγνώστους που προαναφέραμε.
. Αν εφαρμόσουμε τη σχέση
(8.13) για κάθε ένα από τα παραπάνω σημεία καταλήγουμε σε
ένα σύστημα 9 εξισώσεων για τους 9 αγνώστους που προαναφέραμε.