




Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΑΝΑΛΥΣΗ ΣΦΑΛΜΑΤΟΣ
Previous: ΑΝΑΛΥΣΗ ΣΦΑΛΜΑΤΟΣ
Contents
Index
- Η ακριβής τιμή του
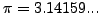 είναι
είναι
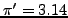 και έστω
μια προσεγγιστική τιμή του
και έστω
μια προσεγγιστική τιμή του 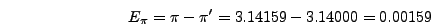 . Το σφάλμα είναι:
. Το σφάλμα είναι:
και το σχετικό σφάλμα:
- An ακριβής τιμή είναι
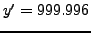 και έστω
μια προσεγγιστική τιμή
και έστω
μια προσεγγιστική τιμή  . Το σφάλμα είναι:
. Το σφάλμα είναι:
και το σχετικό σφάλμα:
- An ακριβής τιμή είναι
 και έστω μια
προσεγγιστική τιμή
και έστω μια
προσεγγιστική τιμή  . Το σφάλμα είναι:
. Το σφάλμα είναι:
και το σχετικό σφάλμα:
Στην πρώτη περίπτωση δεν υπήρχε σημαντική διαφορά μεταξύ των  και
και 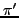 και αμφότερα μπορού να χρησιμοποιηθούν για την εκτίμηση
της ακρίβειας του
και αμφότερα μπορού να χρησιμοποιηθούν για την εκτίμηση
της ακρίβειας του 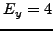 . Στη δεύτερη περίπτωση το σφάλμα
. Στη δεύτερη περίπτωση το σφάλμα 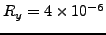 είναι μεγάλο αλλά η κοινή λογική μας οδηγεί στην εκτίμηση ότι η
προσέγγιση δέν είναι κακή και αυτό εκφράζεται καλύτερα μέσω του
σχετικού σφάλματος
είναι μεγάλο αλλά η κοινή λογική μας οδηγεί στην εκτίμηση ότι η
προσέγγιση δέν είναι κακή και αυτό εκφράζεται καλύτερα μέσω του
σχετικού σφάλματος
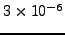 . Τέλος στην τρίτη περίπτωση
το σφάλμα είναι πολύ μικρό
. Τέλος στην τρίτη περίπτωση
το σφάλμα είναι πολύ μικρό
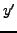 αλλά το σχετικό σφάλμα
είναι μεγάλο και αντιστοιχεί στο 25% της ακριβούς τιμής. Από
την παραπάνω συζήτηση γίνεται προφανές ότι το σχετικό σφάλμα είναι
ένας καλύτερος δείκτης της ακρίβειας μιας προσέγγισης.
αλλά το σχετικό σφάλμα
είναι μεγάλο και αντιστοιχεί στο 25% της ακριβούς τιμής. Από
την παραπάνω συζήτηση γίνεται προφανές ότι το σχετικό σφάλμα είναι
ένας καλύτερος δείκτης της ακρίβειας μιας προσέγγισης.
ΟΡΙΣΜΟΣ: Ενας αριθμός  προσεγγίζει μια ακριβή τιμή
προσεγγίζει μια ακριβή τιμή 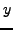 με
με
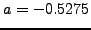 σημαντικά ψηφία αν, ο
σημαντικά ψηφία αν, ο 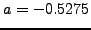 είναι ο μεγαλύτερος αριθμός για τον
οποίο ισχύει:
είναι ο μεγαλύτερος αριθμός για τον
οποίο ισχύει:
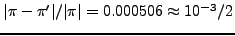 |
(386) |
Kostas Kokkotas
2005-06-13
![]() προσεγγίζει μια ακριβή τιμή
προσεγγίζει μια ακριβή τιμή ![]() με
με
![]() σημαντικά ψηφία αν, ο
σημαντικά ψηφία αν, ο ![]() είναι ο μεγαλύτερος αριθμός για τον
οποίο ισχύει:
είναι ο μεγαλύτερος αριθμός για τον
οποίο ισχύει: