Next: ΣΥΓΚΛΙΣΗ
Up: ΜΕΘΟΔΟΣ NEWTON - RAPHSON
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Θα δοκιμάσουμε μια βελτίωση της μεθόδου Newton-Raphson
προσπαθώντας να επιτύχουμε ταχύτερη σύγκλιση. Για να το επιτύχουμε
θα χρησιμοποιήσουμε ξανά το ανάπτυγμα Taylorκοντά στη ρίζα
της εξίσωσης.
`Εστω ότι
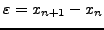 , τότε
, τότε
οπότε, αν θεωρήσουμε ότι
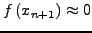 , τότε
, τότε
οπότε λύνοντας ώς το πρώτο από τα 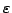 που
βρίσκεται εκτός της αγκύλης καταλήγουμε στην παρακάνω σχέση
που
βρίσκεται εκτός της αγκύλης καταλήγουμε στην παρακάνω σχέση
και αντικαθιστώντας το 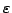 του παρανομαστή απο
την αντίστοιχη σχέση (1.32)της απλής Newton - Raphson
που αναπτύξαμε προηγουμένως, δηλαδή:
του παρανομαστή απο
την αντίστοιχη σχέση (1.32)της απλής Newton - Raphson
που αναπτύξαμε προηγουμένως, δηλαδή:
καταλήγουμε στη σχέση:
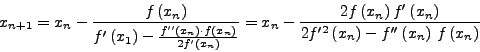 |
(36) |
Είναι προφανές ότι αν θέσουμε 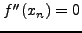 καταλήγουμε στη σχέση
Newton-Raphson, εξίσωση (1.33). Η μέθοδος
αυτή αναφέρεται στη βιβλιογραφία ως μέθοδος του Halley.
καταλήγουμε στη σχέση
Newton-Raphson, εξίσωση (1.33). Η μέθοδος
αυτή αναφέρεται στη βιβλιογραφία ως μέθοδος του Halley.
Subsections
Kostas Kokkotas
2005-06-13
![]() , τότε
, τότε