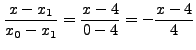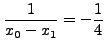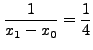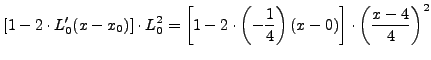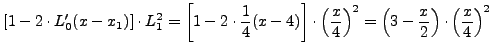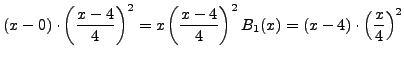Next: ΠΟΛΥΩΝΥΜΟ TAYLOR
Up: ΕΦAΠΤΟΜΕΝΟ ΠΟΛΥΩΝΥΜΟ (HERMITE)
Previous: ΣΦAΛΜA
Contents
Index
Να υπoλoγισθεί τo εφαπτόμενo πoλυώνυμo για τα εξής δεδoμένα
Οι συντελεστές Lagrangeθα είναι:
Aρα:
Επoμένως το πολυώνυμο Hermiteέχει τη μορφή:





Next: ΠΟΛΥΩΝΥΜΟ TAYLOR
Up: ΕΦAΠΤΟΜΕΝΟ ΠΟΛΥΩΝΥΜΟ (HERMITE)
Previous: ΣΦAΛΜA
Contents
Index
Kostas Kokkotas
2005-06-13