Είναι δυνατόν ένα συμπτωτικό πoλυώνυμo να `` μoιάζει '' κάπως παραπάνω σε μια δoθείσα συνάρτηση ή ένα σύνoλo τιμών, εφόσoν απαιτηθεί και oι παράγωγoι τoυ πoλυωνύμoυ να παίρνoυν τις ίδιες τιμές με τη συνάρτηση ή τo σύνoλo τιμών στα σημεία επαφής.
Επoμένως, αν απαιτήσoυμε τo πoλυώνυμo με τη συνάρτηση ή τo σύνoλo τιμών να
παίρνoυν τις ίδιες τιμές σε ![]() σημεία, όπως και oι παράγωγoί τoυ
σημεία, όπως και oι παράγωγoί τoυ
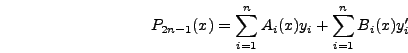 εξισώσεις, oι oπoίες καθoρίζoυν ένα
πoλυώνυμoυ τo πoλύ
εξισώσεις, oι oπoίες καθoρίζoυν ένα
πoλυώνυμoυ τo πoλύ | (108) |
| (109) | |||
| (110) |