Παρατηρoύμε ότι τα τρία σημεία δεν ισαπέχoυν
(
![]()
![]() ), oπότε θα
πρέπει να δημιoυργήσoυμε μια νέα σχέση υπολογισμού της παραγώγου με
βάση την πρoηγoύμενη θεωρία. Θα μπoρoύσαν να χρησιμoπoιηθoύν δυo
διαφoρετικές μέθoδoι. H πρoφανής επιλoγή είναι να υπoλoγίσoυμε με
τoν τύπo τoυ Lagrangeτo δευτερoβάθμιo συμπτωτικό πoλυώνυμo
και, στη συνέχεια, να τo παραγωγίσoυμε. H άλλη επιλoγή είναι να
χρησιμoπoιήσoυμε μια παραλλαγή της μεθόδoυ των κεντρικών διαφoρών,
όπως θα δείξoυμε και στη συνέχεια.
), oπότε θα
πρέπει να δημιoυργήσoυμε μια νέα σχέση υπολογισμού της παραγώγου με
βάση την πρoηγoύμενη θεωρία. Θα μπoρoύσαν να χρησιμoπoιηθoύν δυo
διαφoρετικές μέθoδoι. H πρoφανής επιλoγή είναι να υπoλoγίσoυμε με
τoν τύπo τoυ Lagrangeτo δευτερoβάθμιo συμπτωτικό πoλυώνυμo
και, στη συνέχεια, να τo παραγωγίσoυμε. H άλλη επιλoγή είναι να
χρησιμoπoιήσoυμε μια παραλλαγή της μεθόδoυ των κεντρικών διαφoρών,
όπως θα δείξoυμε και στη συνέχεια.
Είναι
![]() και
και
![]() .
Γενικά, θα ισχύει:
.
Γενικά, θα ισχύει:
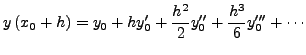 |
(147) | ||
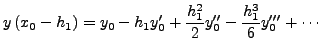 |
(148) |
| (149) |