




Next: Κανόνας τραπεζίου
Up: ΤΥΠΟΙ NEWTON-COTES
Previous: ΣΦΑΛΜΑ
Contents
Index
Με ανάλογο τρόπο βρίσκουμε ότι:
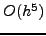 |
(161) |
Δηλαδή, το σφάλμα είναι της αυτής τάξης, 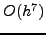 , με την
προηγούμενη μέθοδο όπου χρησιμοποιήσαμε συμπτωτικό πολυώνυμο 2ου
βαθμού. Η ακρίβεια βελτιώνεται εάν διατηρήσουμε και τον επόμενο όρο
στο συμπτωτικό πολυώνυμο, δηλαδή θα παρατηρήσουμε σημαντική βελτίωση
στην ακρίβεια αν χρησιμοποιήσουμε συμπτωτικό πολυώνυμο 4ου βαθμού,
το οποίο έχει ίδιας τάξης σφάλμα με την ολοκλήρωση συμπτωτικού
πολυωνύμου 5ου βαθμού, δηλαδή
, με την
προηγούμενη μέθοδο όπου χρησιμοποιήσαμε συμπτωτικό πολυώνυμο 2ου
βαθμού. Η ακρίβεια βελτιώνεται εάν διατηρήσουμε και τον επόμενο όρο
στο συμπτωτικό πολυώνυμο, δηλαδή θα παρατηρήσουμε σημαντική βελτίωση
στην ακρίβεια αν χρησιμοποιήσουμε συμπτωτικό πολυώνυμο 4ου βαθμού,
το οποίο έχει ίδιας τάξης σφάλμα με την ολοκλήρωση συμπτωτικού
πολυωνύμου 5ου βαθμού, δηλαδή 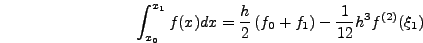 .
.
Στη βιβλιογραφία, οι παραπάνω σχέσεις για την αριθμητική
ολοκλήρωση, που εξάγονται με τη χήση του συμπτωτικού πολυωνύμου,
είναι γνωστοί ως τύποι Newton-Cotes.
Table:
Tύποι Newton-Cotesγια αριθμητική ολοκλήρωση με χρήση
1ης, 2ης και 3ης τάξης συμπτωτικού πολυώνυμου Newton.
|
|
Kostas Kokkotas
2005-06-13