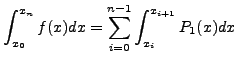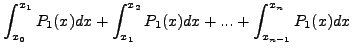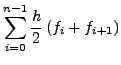Next: ΣΦΑΛΜΑ
Up: ΤΥΠΟΙ NEWTON-COTES
Previous: ΣΦΑΛΜΑ
Contents
Index
Κανόνας τραπεζίου
Αν το διάστημα ολοκλήρωσης 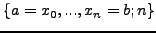 είναι μεγάλο, τότε ορίζουμε μια
διαμέριση
είναι μεγάλο, τότε ορίζουμε μια
διαμέριση
 , όπως φαίνεται στο Σχήμα
5.1.
, όπως φαίνεται στο Σχήμα
5.1.
Figure:
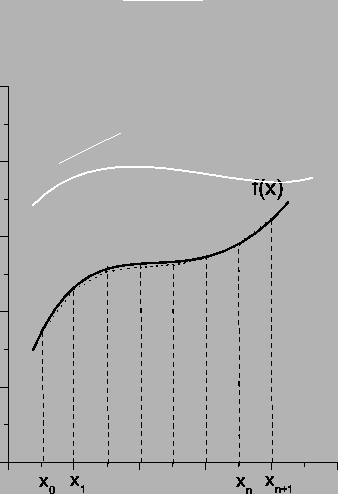
Γραφική απεικόνιση της μέθοδου του τραπεζίου.
|
|
Στην ουσία παίρνουμε το άθροισμα των εμβαδών των επιμέρους
τραπεζίων. Αν τα σημεία είναι ισαπέχοντα, τότε με βάση τα
προηγούμενα:
Οπότε καταλήγουμε στη σχέση:
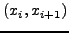 |
(162) |
Ο παραπάνω τύπος για τον αριθμητικό υπολογισμό της τιμής ορισμένων
ολοκληρωμάτων ονομάζεται κανόνας του τραπεζίου.
Subsections
Kostas Kokkotas
2005-06-13
 , όπως φαίνεται στο Σχήμα
5.1.
, όπως φαίνεται στο Σχήμα
5.1.
![]() είναι μεγάλο, τότε ορίζουμε μια
διαμέριση
είναι μεγάλο, τότε ορίζουμε μια
διαμέριση
 , όπως φαίνεται στο Σχήμα
5.1.
, όπως φαίνεται στο Σχήμα
5.1.