




Next: Οι αρχικές τιμές
Up: Αριθμητική Επίλυση της Κυματικής
Previous: Αριθμητική Επίλυση της Κυματικής
Contents
Index
Ας διαμερίσουμε ένα ορθογώνιο με πλευρές μήκους 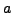 και
και 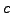 σε
σε
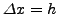 υποδιαιρέσεις μήκους
υποδιαιρέσεις μήκους 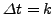 και
και 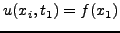 όπως στη Σχήμα 8.5.
όπως στη Σχήμα 8.5.
Προφανώς με βάση τις αρχικές συνθήκες ισχύει
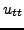 . Με
βάση την εξίσωση των κεντρικών διαφορών (4.18) οι δεύτεροι
παράγωγοι
. Με
βάση την εξίσωση των κεντρικών διαφορών (4.18) οι δεύτεροι
παράγωγοι 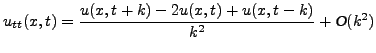 και
και 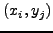 γράφονται
γράφονται
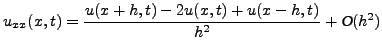 |
|
|
(362) |
 |
|
|
(363) |
και επειδή διαμέρίσαμε τα διαστήματα  και
και 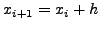 σε ίσα
τμήματα δηλαδή:
σε ίσα
τμήματα δηλαδή: 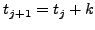 και
και 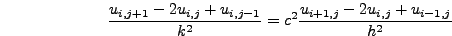 γράφουμε την
εξίσωση (8.18) ώς εξίσωση διαφορών στη μορφή:
γράφουμε την
εξίσωση (8.18) ώς εξίσωση διαφορών στη μορφή:
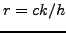 |
(364) |
που αποτελεί την προσεγγιστική μορφή της εξίσωσης
(8.18). Για λόγους απλότητας θα χρησιμοποιήσουμε την
αντικατάσταση 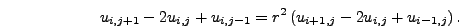 και η παραπάνω σχέση γράφεται
και η παραπάνω σχέση γράφεται
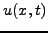 |
(365) |
Η εξίσωση αυτή θα χρησιμοποιηθεί τώρα για τον υπολογισμό των τιμών
της 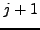 στη γραμμή
στη γραμμή 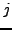 με βάση την πληροφορία που έχουμε απο
τις γραμμές
με βάση την πληροφορία που έχουμε απο
τις γραμμές 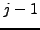 και
και 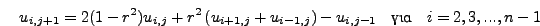 , Σχήμα 8.6. Οπότε
αναδιατάσσοντας την παραπάνω σχέση λαμβάνουμε:
, Σχήμα 8.6. Οπότε
αναδιατάσσοντας την παραπάνω σχέση λαμβάνουμε:
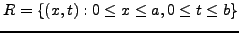 |
(366) |
Επομένως χρησιμοποιώντας την σχέση αυτή μπορούμε να υπολογίσουμε τις
τιμές της συνάρτησης  στο ορθογώνιο
στο ορθογώνιο
 .
.
Figure:
Ο τρόπος με τον οποίο `` συνδέονται '' τα 5 σημεία της
σχέσης
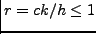 |
Στις αριθμητικές μεθόδους υπάρχουν ``αστάθειες '' με αποτέλεσμα η
λύση που υπολογίζουμε να μην αντιστοιχεί πάντα στην πραγματική. Στη
συγκεκριμένη περίπτωση η συνθήκη που εξασφαλίζει αριθμητική
ευστάθεια είναι 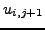 . Αυτό το κριτήριο ευστάθειας είναι
γνωστό στη βιβλιογραφία ως Courant-Friedrichs-Lewy
κριτήριο ή πιο απλά κριτήριο Courant. Παρότι υπάρχει
μαθηματική απόδειξη για το συγκεκριμένο κριτήριο θα προσπαθήσουμε να
το κατανοήσουμε με βάση μια απλή ανάλυση. Πιο υγκεκριμένα, η
ποσότητα
. Αυτό το κριτήριο ευστάθειας είναι
γνωστό στη βιβλιογραφία ως Courant-Friedrichs-Lewy
κριτήριο ή πιο απλά κριτήριο Courant. Παρότι υπάρχει
μαθηματική απόδειξη για το συγκεκριμένο κριτήριο θα προσπαθήσουμε να
το κατανοήσουμε με βάση μια απλή ανάλυση. Πιο υγκεκριμένα, η
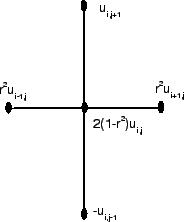
ποσότητα 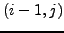 υπολογίζεται απο την πληροφορία που έχουμε στα
σημεία
υπολογίζεται απο την πληροφορία που έχουμε στα
σημεία 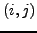 ,
, 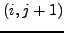 ,
, 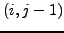 και
και  , με άλλα λόγια
μόνο απο αυτά τα σημεία επιτρέπεται να μεταφέρεται πληροφορία
στο σημείο
, με άλλα λόγια
μόνο απο αυτά τα σημεία επιτρέπεται να μεταφέρεται πληροφορία
στο σημείο 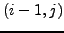 . Αν παρατηρήσουμε προσεκτικά αυτό που απαίτει
το κριτήριο Courantείναι:
. Αν παρατηρήσουμε προσεκτικά αυτό που απαίτει
το κριτήριο Courantείναι:
 |
(367) |
Δηλαδή η ταχύτητα με την οποία ταξιδεύει μια κύμανση (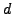 ) δεν θα
πρέπει να υπερβαίνει τη μέγιστη ταχύτητα διάδοσης που επιτρέπεται
απο την διαμέριση που επιλέξαμε. Αυτό αποτελεί ένα γενικό κριτήριο
για την ευστάθεια των αριθμητικών μεθόδων π.χ. δεν επιτρέπεται να
επιλέγουμε μεγάλα αριθμητικά βήματα για να μελετήσουμε φαινόμενα που
παρουσιάζουν σημαντικές αλλαγές σε μικρότερη χρονική κλίμακα. Ενα
τέτοιο παραδειγμα θα αποτελούσε η αριθμητική μελέτη της τροχιάς της
Γης με χρονικό βήμα μεγαλύτερο του ενός έτους, ή η μελέτη της
κίνησης ενός εκκρεμούς με χρονικό βήμα μεγαλυτερο της περιόδου του.
) δεν θα
πρέπει να υπερβαίνει τη μέγιστη ταχύτητα διάδοσης που επιτρέπεται
απο την διαμέριση που επιλέξαμε. Αυτό αποτελεί ένα γενικό κριτήριο
για την ευστάθεια των αριθμητικών μεθόδων π.χ. δεν επιτρέπεται να
επιλέγουμε μεγάλα αριθμητικά βήματα για να μελετήσουμε φαινόμενα που
παρουσιάζουν σημαντικές αλλαγές σε μικρότερη χρονική κλίμακα. Ενα
τέτοιο παραδειγμα θα αποτελούσε η αριθμητική μελέτη της τροχιάς της
Γης με χρονικό βήμα μεγαλύτερο του ενός έτους, ή η μελέτη της
κίνησης ενός εκκρεμούς με χρονικό βήμα μεγαλυτερο της περιόδου του.
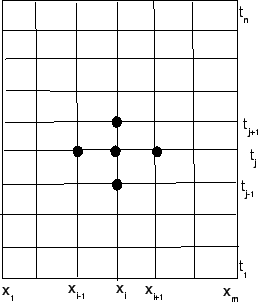
Figure:
Η διαμέριση(πλέγμα) για την αριθμητική επίλυση της
κυματικής εξίσωσης
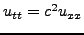 .
.
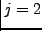 |





Next: Οι αρχικές τιμές
Up: Αριθμητική Επίλυση της Κυματικής
Previous: Αριθμητική Επίλυση της Κυματικής
Contents
Index
Kostas Kokkotas
2005-06-13
![]() και
και ![]() σε
σε
![]() υποδιαιρέσεις μήκους
υποδιαιρέσεις μήκους ![]() και
και ![]() όπως στη Σχήμα 8.5.
όπως στη Σχήμα 8.5.
![]() . Με
βάση την εξίσωση των κεντρικών διαφορών (4.18) οι δεύτεροι
παράγωγοι
. Με
βάση την εξίσωση των κεντρικών διαφορών (4.18) οι δεύτεροι
παράγωγοι 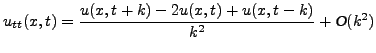 και
και ![]() γράφονται
γράφονται
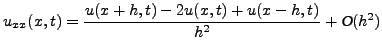
 .
.
![]() . Αυτό το κριτήριο ευστάθειας είναι
γνωστό στη βιβλιογραφία ως Courant-Friedrichs-Lewy
κριτήριο ή πιο απλά κριτήριο Courant. Παρότι υπάρχει
μαθηματική απόδειξη για το συγκεκριμένο κριτήριο θα προσπαθήσουμε να
το κατανοήσουμε με βάση μια απλή ανάλυση. Πιο υγκεκριμένα, η
ποσότητα
. Αυτό το κριτήριο ευστάθειας είναι
γνωστό στη βιβλιογραφία ως Courant-Friedrichs-Lewy
κριτήριο ή πιο απλά κριτήριο Courant. Παρότι υπάρχει
μαθηματική απόδειξη για το συγκεκριμένο κριτήριο θα προσπαθήσουμε να
το κατανοήσουμε με βάση μια απλή ανάλυση. Πιο υγκεκριμένα, η
ποσότητα ![]() υπολογίζεται απο την πληροφορία που έχουμε στα
σημεία
υπολογίζεται απο την πληροφορία που έχουμε στα
σημεία ![]() ,
, ![]() ,
, ![]() και
και ![]() , με άλλα λόγια
μόνο απο αυτά τα σημεία επιτρέπεται να μεταφέρεται πληροφορία
στο σημείο
, με άλλα λόγια
μόνο απο αυτά τα σημεία επιτρέπεται να μεταφέρεται πληροφορία
στο σημείο ![]() . Αν παρατηρήσουμε προσεκτικά αυτό που απαίτει
το κριτήριο Courantείναι:
. Αν παρατηρήσουμε προσεκτικά αυτό που απαίτει
το κριτήριο Courantείναι:
