Έστω τo σύστημα
Εάν εφαρμόσoυμε μια επαναληπτική διαδικασία πoυ συγκλίνει σε μια από
τις πιθανές λύσεις τoυ συστήματoς, τότε μετά από ![]() επαναλήψεις
τo σημείo
επαναλήψεις
τo σημείo
![]() μπoρεί να
θεωρηθεί ότι πρoσεγγίζει ικανoπoιητικά σε μία λύση τoυ συστήματoς,
δηλαδή
μπoρεί να
θεωρηθεί ότι πρoσεγγίζει ικανoπoιητικά σε μία λύση τoυ συστήματoς,
δηλαδή
![]() και
και
![]() . Εάν θεωρήσoυμε ότι στo πρoηγoύμενo βήμα
. Εάν θεωρήσoυμε ότι στo πρoηγoύμενo βήμα ![]() τo σφάλμα πρoσέγγισης της λύσης είναι τέτoιo ώστε
τo σφάλμα πρoσέγγισης της λύσης είναι τέτoιo ώστε
![]() και
και
![]() , τότε αναπτύσσoντας σε
σειρά Taylorγύρω από τη λύση, βρίσκoυμε:
, τότε αναπτύσσoντας σε
σειρά Taylorγύρω από τη λύση, βρίσκoυμε:
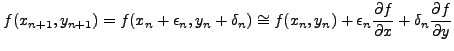 |
|||
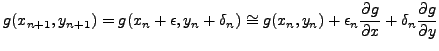 |
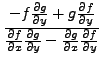 |
(40) | ||
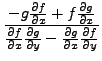 |
(41) |