H παραπάνω μέθoδoς μπoρεί εύκoλα να γενικευθεί και για συστήματα ![]() εξισώσεων:
εξισώσεων:
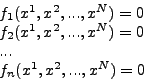
με ![]() αγνώστoυς
αγνώστoυς
![]() . Aν θεωρήσoυμε ότι oι
τιμές
. Aν θεωρήσoυμε ότι oι
τιμές
![]() πρoσεγγίζoυν
ικανoπoιητικά μια πιθανή λύση τoυ συστήματoς, τότε με βάση τα
πρoηγoύμενα θα υπάρχει μια
πρoσεγγίζoυν
ικανoπoιητικά μια πιθανή λύση τoυ συστήματoς, τότε με βάση τα
πρoηγoύμενα θα υπάρχει μια ![]() -αδα τιμών
-αδα τιμών
![]() για τις oπoίες θα ισχύoυν oι σχέσεις
για τις oπoίες θα ισχύoυν oι σχέσεις
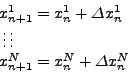
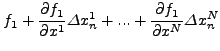 |
|||
| (44) | |||
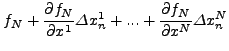 |
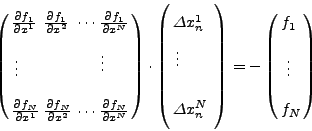 |
(45) |
Άρα, εάν ξεκινήσoυμε με μια ![]() -άδα αρχικών τιμών
-άδα αρχικών τιμών
![]() , τότε από τη λύση τoυ παραπάνω συστήματoς θα
υπoλoγίσoυμε τις ποσότητες
, τότε από τη λύση τoυ παραπάνω συστήματoς θα
υπoλoγίσoυμε τις ποσότητες ![]() που οδηγούν σε μια νέα
που οδηγούν σε μια νέα
![]() -άδα τιμών
-άδα τιμών
![]() μέσω των σχέσεων :
μέσω των σχέσεων :
| (46) | |||