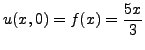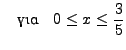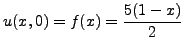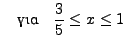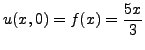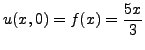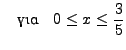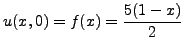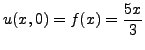next up previous contents index
Next: ΠΑΡΑΒΟΛΙΚΕΣ ΕΞΙΣΩΣΕΙΣ Up: Αριθμητική Επίλυση της Κυματικής Previous: Οι αρχικές τιμές   Contents   Index

ΠΡΟΒΛΗΜΑΤΑ

  1. Να λυθεί η κυματική εξίσωση της παλλόμενης χορδής
    \begin{displaymath} u_{tt}(x,t)=4 u_{xx}(x,t) \quad \mbox{\rm για} \quad 0<x<1 \quad \mbox{\rm και} \quad 0<t<0.5 \nonumber \end{displaymath}  

    με οριακές συνθήκες
    $\displaystyle u(0,t)=0 \quad \mbox{\rm και} \quad u(1,t)=0$   $\displaystyle \quad \mbox{\rm για} \quad 0\leq t \leq 1$  
    $\displaystyle u(x,0)=f(x)={5 x \over 3}$   $\displaystyle \quad \mbox{\rm για} \quad 0\leq x \leq {3\over 5}$  
    $\displaystyle u(x,0)=f(x)={5 (1-x) \over 2}$   $\displaystyle \quad \mbox{\rm για} \quad {3\over 5}\leq x \leq 1$  
    $\displaystyle u_t(x,0)=g(x)=0$   $\displaystyle \quad \mbox{\rm για} \quad 0 < x < 1$  

  2. Να επιβεβαιωθεί αναλυτικά ότι η 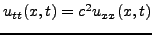$u(x,t)=\sin(n\pi x)\cos(cn\pi t)$ είναι λύση της εξίσωσης 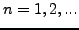$u_{tt}(x,t)=c^2 u_{xx}(x,t)$ για κάθε θετικό ακέραιο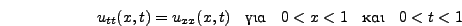 $n=1, 2, ...$

  3. Να λυθεί η κυματική εξίσωση της παλλόμενης χορδής
    \begin{displaymath} u_{tt}(x,t)= u_{xx}(x,t) \quad \mbox{\rm για} \quad 0<x<1 \quad \mbox{\rm και} \quad 0<t<1 \nonumber \end{displaymath}  

    με οριακές συνθήκες
    $\displaystyle u(0,t)=0 \quad \mbox{\rm και} \quad u(1,t)=0$   $\displaystyle \quad \mbox{\rm για} \quad 0\leq t \leq 1$  
    $\displaystyle u(x,0)=f(x)=\sin(\pi x)$   $\displaystyle \quad \mbox{\rm για} \quad 0\leq x \leq 1$  
    $\displaystyle u_t(x,0)=g(x)=0$   $\displaystyle \quad \mbox{\rm για} \quad 0 < x < 1$  

  4. Δοκιμάστε στα παραπάνω προβλήματα τιμές του 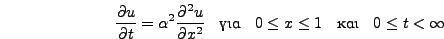$r$ μεγαλύτερες και μικρότερες του 1 για να μελετήσετε την ευστάθεια της μεθόδου.


Kostas Kokkotas 2005-06-13