




Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΑΡΙΘΜΗΤΙΚΗ ΟΛΟΚΛΗΡΩΣΗ
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Γνωρίζουμε από τον Ολοκληρωτικό Λογισμό ότι για μια συνάρτηση 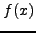 υπάρχει μια κατάλληλη τιμή
υπάρχει μια κατάλληλη τιμή 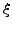 στο διάστημα ολοκλήρωσης
στο διάστημα ολοκλήρωσης 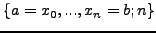 ούτως ώστε να ισχύει (θεώρημα μέσης τιμής):
ούτως ώστε να ισχύει (θεώρημα μέσης τιμής):
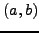 |
|
|
(178) |
Αν το γενικεύσουμε, θα μπορούσαμε να προσεγγίσουμε ένα διάστημα με
ένα γραμμικό συνδυασμό τιμών της
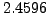 εντός του
διαστήματος
εντός του
διαστήματος
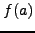 . Επίσης, θα μπορούσαμε να συνδυάσουμε
ακόμη και παραγώγους της
. Επίσης, θα μπορούσαμε να συνδυάσουμε
ακόμη και παραγώγους της
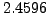 σ’ αυτό το διάστημα.
Στην πιο απλή περίπτωση, προσεγγίζουμε το ολοκλήρωμα με δυο μόνο
τιμές της συνάρτησης, την
σ’ αυτό το διάστημα.
Στην πιο απλή περίπτωση, προσεγγίζουμε το ολοκλήρωμα με δυο μόνο
τιμές της συνάρτησης, την 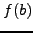 και την
και την 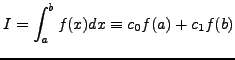 . Οπότε γράφουμε:
. Οπότε γράφουμε:
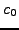 |
|
|
(179) |
Οι τιμές των 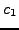 ,
, 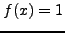 εξαρτώνται από την
εξαρτώνται από την 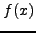 αλλά και από τις
τιμές των
αλλά και από τις
τιμές των 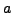 και
και 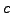 .
.
Για να είναι αληθής η παραπάνω σχεση, θα πρέπει η 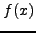 να είναι
είτε σταθερή συνάρτηση είτε γραμμική ως προς
να είναι
είτε σταθερή συνάρτηση είτε γραμμική ως προς 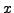 . Οπότε, αν
αντικαταστήσουμε μια φορά για
. Οπότε, αν
αντικαταστήσουμε μια φορά για 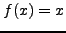 και στη συνέχεια για
και στη συνέχεια για 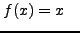 , τα ολοκληρώματα υπολογίζονται ακριβώς και επομένως θα
δημιουργήσουμε δύο εξισώσεις για τους δύο αγνώστους
, τα ολοκληρώματα υπολογίζονται ακριβώς και επομένως θα
δημιουργήσουμε δύο εξισώσεις για τους δύο αγνώστους 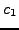 και
και 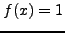 .
Δηλαδή:
.
Δηλαδή:
Οπότε, εύκολα βρίσκουμε ότι:
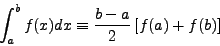 |
(182) |
Άρα
![\begin{displaymath}
\int_a^b f(x)dx \equiv \frac{b-a}{2}\left[ f(a)+f(b)\right]
\end{displaymath}](img1231.png) |
(183) |
Ουσιαστικά, έχουμε δημιουργήσει ξανά τον «κανόνα του τραπεζίου», που
δίνει ακριβή αποτελέσματα για συναρτήσεις που παριστάνουν ευθείες.
Αν συνεχίσουμε δημιουργώντας μία σχέση με τρεις όρους παρόμοια με την
(5.30), δηλαδή,
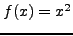 |
(184) |
τότε η παραπάνω σχέση μπορεί να είνα ακριβής μόνο αν η 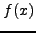 ήταν πολυώνυμο το πολύ 2ου βαθμού. Οπότε, θέτω
ήταν πολυώνυμο το πολύ 2ου βαθμού. Οπότε, θέτω 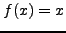 ,
, 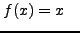 και
και 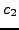 και ολοκληρώνοντας για την κάθε μια συνάρτηση
δημιουργώ ένα σύστημα τριών εξισώσεων για τους τρείς αγνώστους
και ολοκληρώνοντας για την κάθε μια συνάρτηση
δημιουργώ ένα σύστημα τριών εξισώσεων για τους τρείς αγνώστους
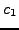 ,
, 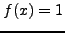 και
και 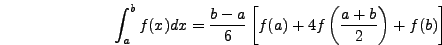 , από τη λύση του οποίου καταλήγω στην
εξίσωση:
, από τη λύση του οποίου καταλήγω στην
εξίσωση:
![\begin{displaymath}
\int_a^b f(x)dx = \frac{b-a}{6}\left[ f(a) +
4f\left(\frac{a+b}{2}\right) + f(b)\right]
\end{displaymath}](img1235.png) |
(185) |
που στην ουσία είναι ο κανόνας του Simpsonγια τρία σημεία.
Θα μπορούσαμε εύκολα να επεκτείνουμε την παραπάνω διακασία,
προσθέτοντας και τις πρώτες παραγώγους της συνάρτησης σε κάποια
σημεία του διαστήματος ολοκλήρωσης, για παράδειγμα:
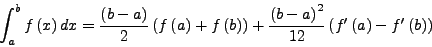 |
(186) |
οπότε θα πρέπει να καταλήξω σε ένα σύστημα με τέσσερις άγνωστες
ποσότητες που θα μας οδηγήσει στη σχέση:
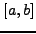 |
(187) |
Δηλαδή, θα υπολογίσουμε το ολοκλήρωμα μόνο με βάση τις τιμές της
συνάρτησης και της παραγώγου της στα άκρα του διαστήματος ![$[a,b]$](img1238.png) . Η
σχέση αυτή γενικεύεται στον τύπο των Euler-Maclaurin(πώς?)
. Η
σχέση αυτή γενικεύεται στον τύπο των Euler-Maclaurin(πώς?)
που είναι μια εξαιρετικά ακριβής μέθοδος και στην ουσία
βελτιώνει το αποτέλεσμα με μόνο 6 επιπλέον υπολογισμούς της 1ης, 3ης
και 5ης παραγώγου της συνάρτησης στα άκρα του διαστήματος.
Subsections





Next: ΠΑΡΑΔΕΙΓΜΑ
Up: ΑΡΙΘΜΗΤΙΚΗ ΟΛΟΚΛΗΡΩΣΗ
Previous: ΠΑΡΑΔΕΙΓΜΑ
Contents
Index
Kostas Kokkotas
2005-06-13
![]() υπάρχει μια κατάλληλη τιμή
υπάρχει μια κατάλληλη τιμή ![]() στο διάστημα ολοκλήρωσης
στο διάστημα ολοκλήρωσης ![]() ούτως ώστε να ισχύει (θεώρημα μέσης τιμής):
ούτως ώστε να ισχύει (θεώρημα μέσης τιμής):
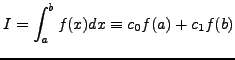 . Οπότε γράφουμε:
. Οπότε γράφουμε:
![]() να είναι
είτε σταθερή συνάρτηση είτε γραμμική ως προς
να είναι
είτε σταθερή συνάρτηση είτε γραμμική ως προς ![]() . Οπότε, αν
αντικαταστήσουμε μια φορά για
. Οπότε, αν
αντικαταστήσουμε μια φορά για ![]() και στη συνέχεια για
και στη συνέχεια για ![]() , τα ολοκληρώματα υπολογίζονται ακριβώς και επομένως θα
δημιουργήσουμε δύο εξισώσεις για τους δύο αγνώστους
, τα ολοκληρώματα υπολογίζονται ακριβώς και επομένως θα
δημιουργήσουμε δύο εξισώσεις για τους δύο αγνώστους ![]() και
και ![]() .
Δηλαδή:
.
Δηλαδή:
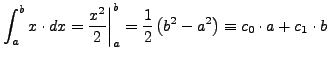
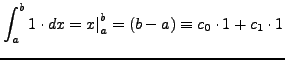
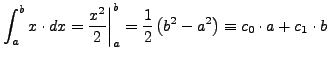
![$[a,b]$](img1238.png) . Η
σχέση αυτή γενικεύεται στον τύπο των Euler-Maclaurin(πώς?)
. Η
σχέση αυτή γενικεύεται στον τύπο των Euler-Maclaurin(πώς?)